[경제수리통계학] 7. Sampling distribution: univariate

1. Random Sample

모집단에 대해 복원반복추출을 진행한다. 복원반복추출은 두가지 특성을 가진다.

첫째, 추출된 random variable(r.v)를 기록한 뒤 다시 모집단에 넣어 "복원"한다.

둘째, 복원되었기에 매 추출시행 때마다 특정 r.v가 추출될 확률이 고정된 체로 "반복"된다.

이 때문에 추출된 sample의 r.v는 independent & identically distributed, 즉 i.i.d라는 성질을 갖게 된다.

이 i.i.d가 sample을 통한 population 추정의 핵심가정이 된다. 

 

이 때, independent는 이전에 추출된 r.v가 배제되지 않고 다시 모집단에 속한 체로 표본추출이 시행되었다는 점에서 이전의 사건과 현재의 사건간의 확률적 의존이 없음을 뜻한다. identically distributed는 복원추출의 환경이기 때문에 매번 X1, X2, X3 등의 r.v가 추출된 확률은 같다는 뜻이다. 따라서 이 때 확률함수 f(x)는 항시 같은 것이 사용된다. 

이러한 특성 때문에 random sample의 joint density function은 f(x1)f(x2)f(x3)...f(xn)으로 표기가능하다. 

 

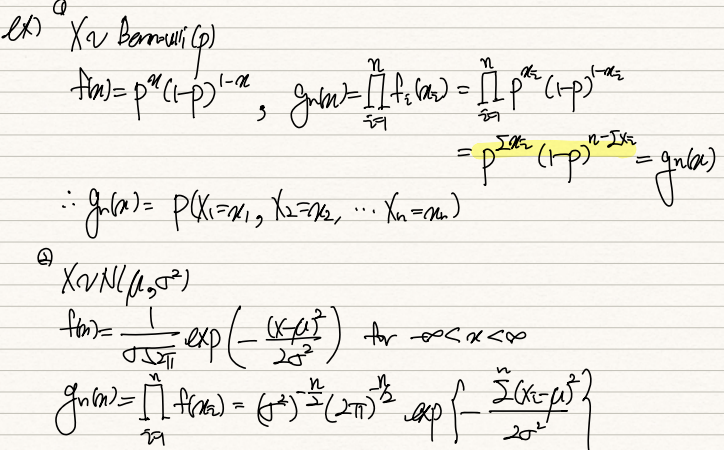
위는 random sample의 r.v X가 베르누이분포를 따른다고 가정한 경우와 정규분포를 따른다고 가정한 경우다. 

시행횟수 n만큼 f(x)가 곱해진 것이 joint density function g(x)이다. 

 

2. Sample Statistics

Sample Statistics, 즉 표본통계량은 위와 같다. MGF(적률생성함수)를 통해 도출해낼 수 있다. 

 

1) Sample mean

우선 표본평균이 있다. 표본평균의 분포는 두가지 변수에 의존한다. 바로 모집단의 분산과 표본수다. 

통상적으로 E(X-bar)=μ, V(X-bar)=σ^2/n이다. 

 

"Sample Mean Theorem"이란 것이 존재한다. 

random sample된 size=n의 표본집단에서, 어떠한 분포를 갖던 상관없이 E(X-bar)=μ, V(X-bar)=σ^2/n이란 것이다. 

만약 n의 크기가 충분히 크다면 V(X-bar)가 0에 수렴하게 되면서, E(X-bar)의 분포는 μ 근방으로 좁아지게 되어 예측정확도가 높아지게 될 것이다.

 

2) Sample raw moment

Sample mean을 도출하는데 사용된 Sample raw moment가 존재한다. 여기서 다소 헷갈리는 부분이 왜 moment의 평균을 구하냐는 것이다. 절차를 따져보면 이는 당연한 소리다. 

a. population set에서 Xi라는 r.v를 random sampling 절차를 통해 추출해낸다.

b. 이들을 모두 sum up하고 나눠주어 그 평균값을 구하는데, 이것이 바로 Mr', 즉 Sample raw moment다. 

c. 동작업을 여러번 해주면 Mr'는 일정한 분포를 그리게 되는데, 그 분포의 모양과는 무관하게 Mr', 즉 sample mean의 평균값은 모집단의 평균값과 같으며, 분산은 sample mean variance와 같음을 알 수 있다. 

복잡해보이지만 Sample mean Theorem을 구하기 위한 방법인 것이다. 

 

3) Sample central moment about population mean

그렇다면 이번엔 Sample central moment about pop mean을 살펴보자.

Mr*는 r.v를 추출 후 이를 모평균을 차감한 값을 평균한 것이다. μ가 Xi에 영향을 주지 않는 constant라는 점에서 이는 Sample mean Thm의 적용대상이 된다. 따라서 Mr*의 평균값은 μ_r, V(Mr*)=(E(M2*)-E(M1*)^2)/n이다. 

r=1인 경우, E(M1*)=μ_1=0이 된다. r=2은 E(M2*)=μ_2=V(X)가 된다. 이를 V(Mr*)에 대입시, V(M1*)=V(X)/n이 도출된다. 

 

4) Sample central moment about sample mean

그렇다면 Sample Central moment about sample mean은 어떨까?

이전과 달라진 점은 μ 대신 표본평균값인 X-bar가 포함된 것 뿐이다. 다만 이는 완전 다른 결과로 이어진다.

Xi와 X-bar의 차를 Zi라고 설정하자. Z1과 Z2간의 공분산을 구하는 경우, C(X1,X2)는 i.i.d 특성에 의해 0이 되지만, X1과 X-bar, X2와 X-bar의 공분산은 V(X-bar)값을 갖게 된다. 이는 상수로 취급했던 모평균과 달리 X-bar는 X1이 속하여 둘 간의 상관성이 있다고 판단하기 때문이다. 따라서 Xi가 i.i.d의 특성을 갖더라도 Xi-Xbar를 통해 정규화한 값인 Zi는 서로간에 i.i.d가 성립하지 않는다. 그래서 Zi에 대해선 Sample mean Thm이 적용되지 않는다.

 

그러나 sample size n을 극도로 늘릴 경우 i.i.d가 아닐지라도 sample mean thm이 근사적으로 사용될 수 있다. 

M2 적률함수를 식조작을 해주면, M2*-(u-Xbar)^2이 도출된다.

M2*은 Sample central moment about pop. mean이기 때문에 (Xi-μ)는 i.i.d의 특성을 지닌다. 이를 Zi로 설정하여 Sample mena Theorem을 적용하면 E(Zi)=σ^2, V(Zi)=μ^4-σ^4가 도출된다. 

 

다시 돌아와서, M2=M2*-(μ-Xbar)^2의 양변에 Expectation을 씌우면, σ^2-V(Xbar)가 도출되고, 이는 즉 (n-1)(σ^2)/n이다. 만약 n이 매우 큰 숫자일 때 모분산에 수렴하기 때문에, sample central moment about sample mean(r=2) 또한 모분산으로 수렴하게 된다. 대수의 법칙이 작용하는 것이다. 

 

3. Sampling distribution: the porbability distribution of sample statistic

1) chi-square distribution

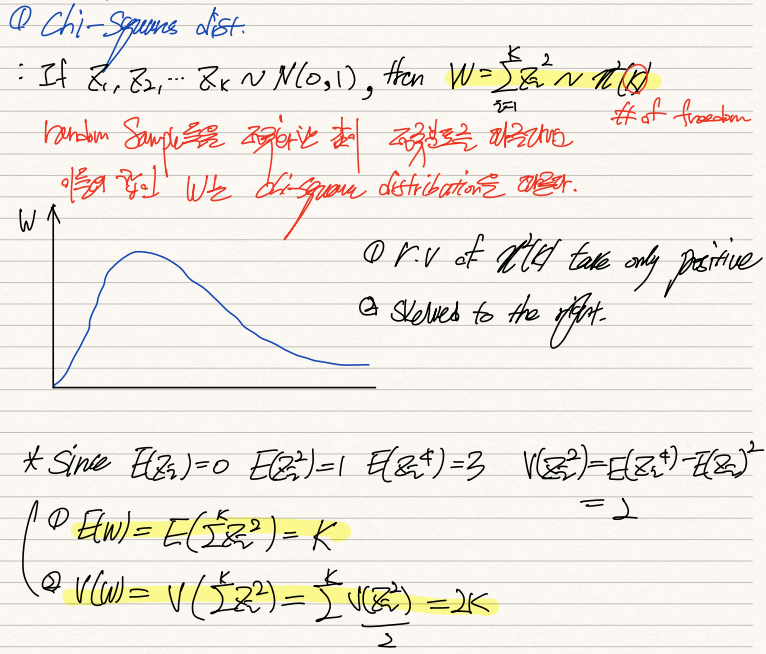
대수의 법칙에 의거하여 Xi-Xbar의 제곱을 평균내준 값도 n이 충분히 크다면 모분산에 수렴한다는 것을 파악했다.

이제 카이분포를 통해 이들 (Xi-Xbar)/표본분산, 즉 정규화된 Zi제곱의 합의 분포를 파악해보자. 

 

카이분포를 통해 우리가 확인하고자 하는 것은 '분산의 분포'다. 위 예시의 절차를 생각해보자.

a. 특정 차의 연비(X)가 N(18, 4)의 정규분포를 따른다고 가정하자.

b. 소비자가 사측의 주장인 "평균=18, 분산=4"를 검증하기 위해 n=16의 sample을 추출하여 표본평균을 구했다. 

c. 만약 사측에서 추정한 것이 맞다면 Xbar가 N(18,4/16)의 정규분포를 따라야 한다. 

d. 표본평균이 16.8로 추정되었다면 검증을 통해 이 평균값이 신뢰구간 내 존재하는 수치인지 확인할 수 있다. 

e. 그리고 어떤이는 해당 표본의 분산이 모분산을 따르는지 검증하기 위해 카이분포를 활용한다. 

 

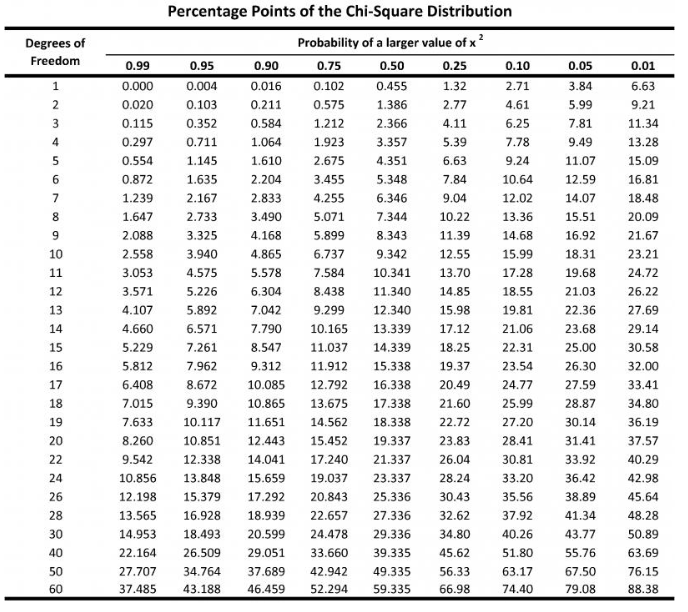
예를 들어, 모분산이 0.8인 정규분포로부터 n=9의 random sample을 추출했다고 가정하자. 90% 신뢰도로 표본분산이 유의미한 값을 갖기 위해선 카이분포값이 2.73과 15.51 사이면 된다. 분산은 0.273, 1.551 사이면 된다. 

 

비슷한 예시. 음료수 회사에서 음료캔 무게의 분산을 2로 추정하고 있다. 이를 맞는지 확인하려고 한다. 

표본의 크기가 25일 때 카이분포값이 36.42를 넘긴다면 신뢰할 수 없는 표본분산인 것이다. 

 

2) student's t-distribution

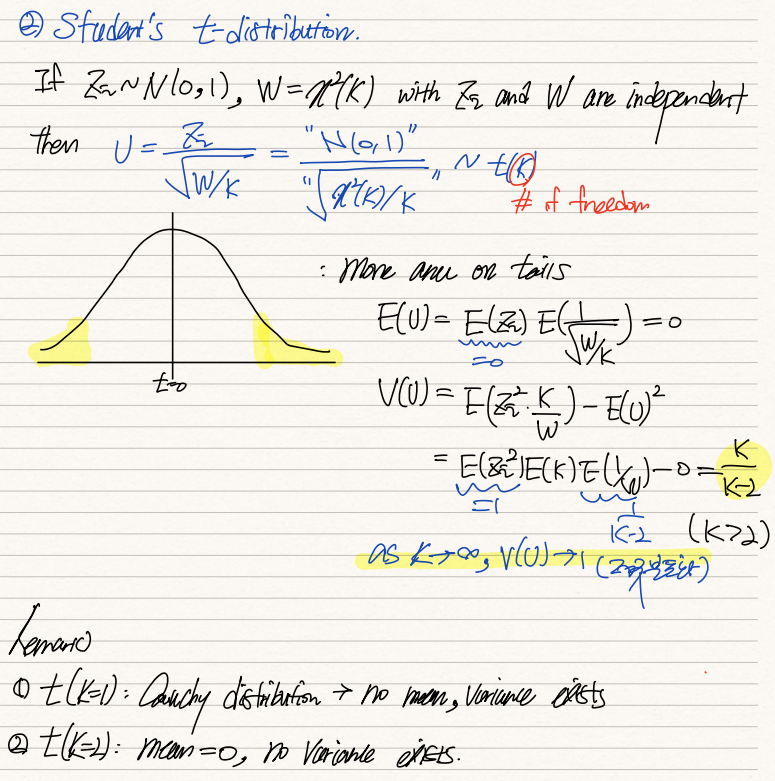
Z값과 W값이 서로 독립적이라면, U=Z/(W/k)^(-1/2)이며 이 값은 k의 자유도를 갖고 t분포를 따른다. t분포의 U를 식조작할 경우 모분산이 상쇄되고 표본분산의 루트값, s만 남기 때문에 모분산에 대한 정보가 없는 경우 활용된다. 

t분포의 평균, E(U)는 0이며, V(U)는 k/(k-2)이다. 따라서 이 분포는 표본의 크기가 크면 클수록 그 분포가 정규분포와 유사해지는 속성을 갖는다. 

 

 

4. Sampling distribution from normal distribution

만약 모집단이 정규분포를 따른다고 가정할때, 우리는 표본집단으로부터 다음의 특성을 관찰할 수 있다. 

첫째, 표본평균의 분포 또한 정규분포를 따르며, 이 때 평균값은 모평균, 분산은 모분산/n이다. 

둘째, r.v를 표본평균에 대해 정규화해준 값의 합을 우리는 W로 표기하며, 이는 식을 조작할 경우 표본분산에 대한 정보를 제공함을 확인할 수 있다. n이 크면 클수록 표본분산이 모분산에 수렴하는 특성을 갖고 있기 때문에, 주어진 신뢰도 아래 n이 커질수록 표준분산이 쓸모없는 값이라는 것을 확인해줄 카이분포값이 커짐을 확인할 수 있다. 즉, 다시말해 표본의 크기가 1인 경우엔 그 하나의 값이 모분산과 비교했을 때 무의미한 값일 확률이 높기에 카이분포값이 매우 작아야하지만, n이 커질수록 모분산에 근사하기 때문에 카이분포값이 커져서 표본분산이 쓸모없는 값이라고 판단하기 어려워진다는 것이다.

셋째, 표본분산과 표본평균은 서로 독립적이다.

넷째, 따라서 Z와 W가 독립적이기 때문에 t분포를 시행할 수 있으며, t분포는 결국 모분산을 모르기 때문에 하는 test다.