
G가 graph일 때, 모든 vertices에 대한 sigma sum of d(v)는 2*|E(G)|다. 이를 handshaking lemma라 부른다.
여기서 파생된 corollary: 홀수인 d(v)의 갯수는 짝수여야만한다.
예시1. 홀수인 degree of vertices가 4개다.
예시2. 홀수인 d(v)가 6개다.

corollary를 증명하기 위해서,
2|E(G)|는 mod2일때 remainder=0 or 1로 나뉜다.
2|E(G)|의 mod2는 0이고 remainder = 0일때도 0,

degree seq은 (0,1,2,2,2,2,2,3)과 같이 특정 그래프의 degree를 나열한 수열이다.

예시

Handshaking Lemma의 cor에 의해 홀수 degree의 갯수는 짝수다.

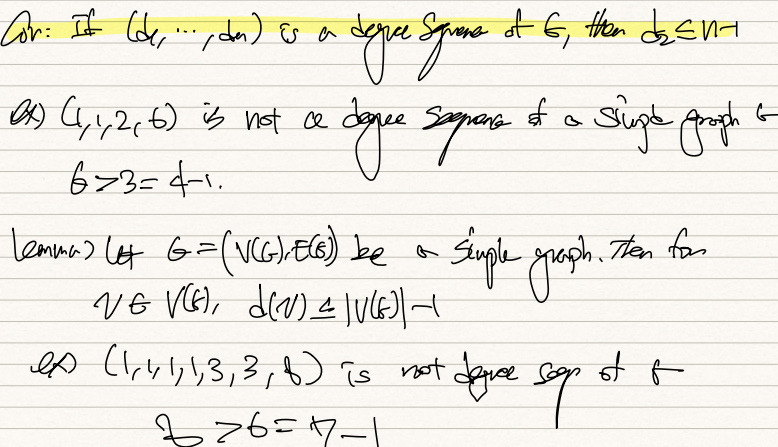
그래프의 degree는 무조건 |V(G)|-1 이하여야 한다.

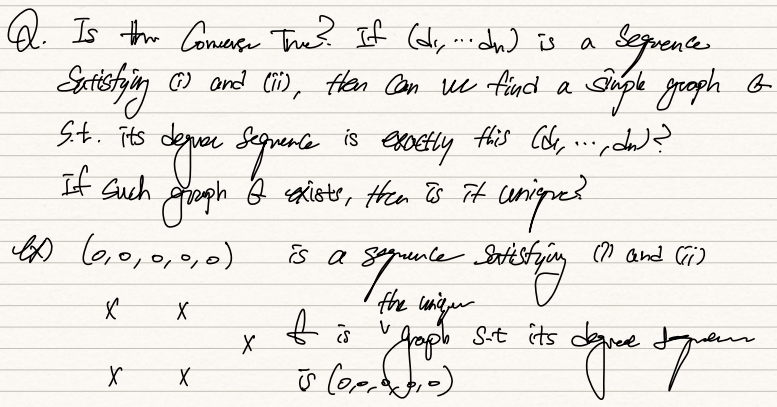

(1,1,2,2,2)
특정 degree seq를 가지는 graph는 여러개일수 있다.

degree seq가 주어졌을 때 |E(G)|를 찾는법,
handshaking lemma를 사용하면 sigma sum of degree = 2|E(G)|
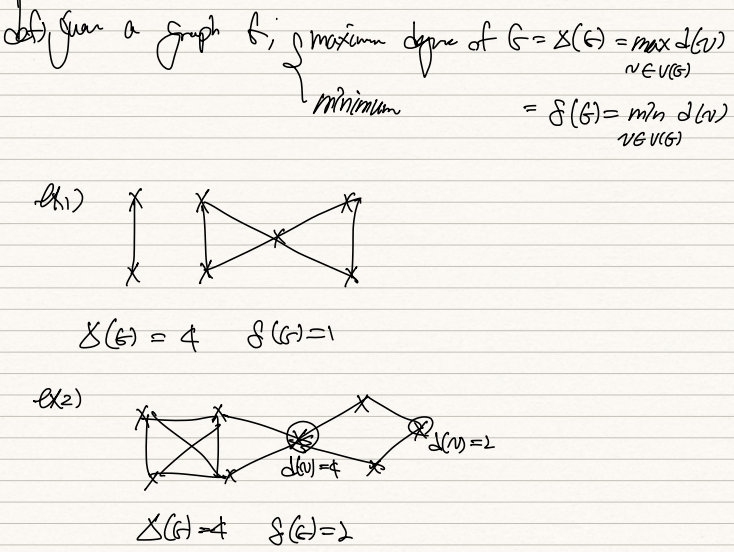
DEL(G) = max d(v)
del(G) = min d(v)

G가 n개의 vertices를 가진 simple graph라면, |V(G)|=n이고, DEL(G) <= n-1다. 그 스스로는 빠지기 때문.
만약 d(v) = d(u) for all u,v in V(G)라면 G는 regular graph다. 똑같이, del(G) = DEL(G)라면 G는 regular graph다.

null graph는 E(G)가 공집합인 그래프다. 이 경우 모든 d(v)가 0으로 같기 때문에 regular graph다.
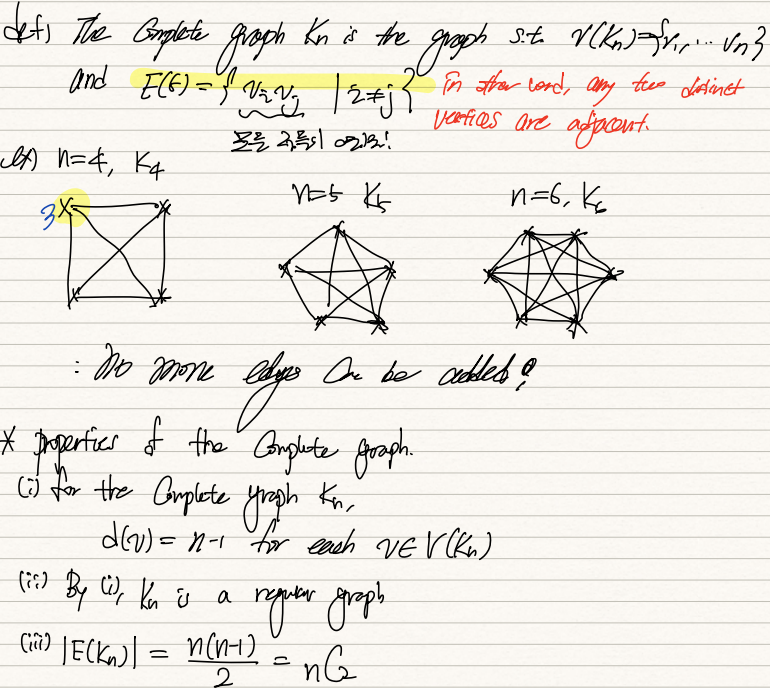
Kn은 complete graph다. Complete graph는 {v1, ..., vn}으로 구성된 Vertices set, E(G) = {vivj | i != j}를 가진다. 즉, 모든 vertices가 상호간에 연결된 완전한 그래프다.
Kn의 특성은 다음과 같다.
1) Kn의 d(v) = n-1
2) Kn은 regular graph (del(G) = DEL(G))
3) |E(Kn)| = n(n-1)/2 = nC2

handshaking lemma에 의해 2|E(Kn)| = sigma sum of degree = sigma sum of (n-1) = n(n-1)

prop. Kn의 |E(G)|는 모든 simple graph 중 가장 크다.
1) d(v) = n-1 for all v in v(Kn)
2) Kn is regular graph
3) |E(Kn)| = nC2
4) degree seq of Kn is (n-1, n-1, ...) * n개
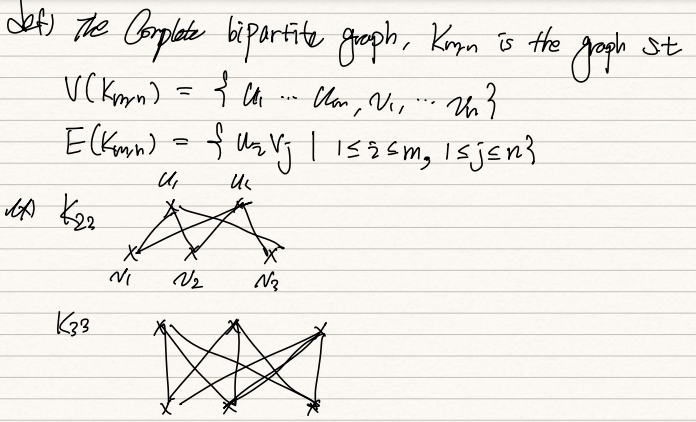
K_m,n은 complete bipartite graph(이분그래프)다. K_m,n은 V(Km,n) = {u1, ... , um, v1, ... vn}이고 E(Km,n)={ui,vj| for all i,j}다.

Complete bipartite graph의 특징은 다음과 같다.
1) Km,n은 ismorphic to Kn,m이다.
2) d(ui) = n, d(vj) = m이다.
3) degree seq of Km,n(m<=n)은 (n,n,n... (m개) , m,m...(n개))로 구성된다.
4) |E(Km,n)| = mn (pf. handshaking lemma)

Complete multipartite graph는 bi가 아닌 multi라는 점만 다르다.
'수학 > 이산수학(Graph Theory)' 카테고리의 다른 글
| [이산수학] (7) Connection (0) | 2022.05.18 |
|---|---|
| [이산수학] (6) Subgraphs (0) | 2022.04.20 |
| [이산수학] (4) Fundamentals of Graph Thoery (0) | 2022.04.20 |
| [이산수학] (3) Partition (0) | 2022.04.20 |
| [이산수학] (2) Relations (0) | 2022.04.19 |



