
Dirac's Thm:
G가 |V(G)| = n >= 3 인 그래프일 때, del(G) >= n/2라면 G는 Hamiltonian이다.
*del(G) : minimal degree of graph G
pf) Thm이 틀렸다고 가정해보자. 그렇다면 del(G) >= n/2인데 G가 Hamiltonian이 아니란 뜻이다.
우선 G에서 가장 긴 length를 가진 Path를 하나 선정한다.

u,v in V(G) s.t u is not adjacent to v인 u,v를 찾아보자. 이 경우 G+uv는 Hamiltonian이다.
이 뜻은 G+uv에는 Hamiltonian Cycle이 있다는 뜻이고, G에는 없었던게 uv를 추가하면서 생기는것이니 Cycle에 uv는 꼭 포함되어야만 한다.




Bondy & Chvatal Thm)
만약 G가 |V(G)|=n인 그래프라고 가정해보자. u,v in V(G), u!=v는 uv라고 가정할 때, d(u)+d(v) >= n 이다.
그렇다면 G는 Hamiltonian이다. iff G+uv 는 Hamiltonian이다.
pf)
=> : G는 Hamiltonian Cycle C를 가진다. C는 G+uv에서도 Hamiltonian이다. 고로 G+uv도 Hamiltonian이다.
<= : G+uv가 Hamiltonian이고, G가 아니라고 가정해보자. Dirac's Thm에 의하면, d(u) + d(v) <= n-1 이란 사실은 d(u)+d(v) >= n인 가정과 배치된다. 따라서 G 또한 Hamiltonian이다.

G에 edge를 더하면 Hamiltonian Cycle이 새로이 생길 가능성이 생긴다.

def) G의 Closure, C(G)는 non-adjacent vertices를 결합함으로써 얻어지는 최종결과물이다. 이 때 양 vertices의 합은 적어도 |V(G)| 만큼은 되어야한다.
non-adjacent vertices의 degree합이 n을 넘으니까 G는 Hamiltonian이다.
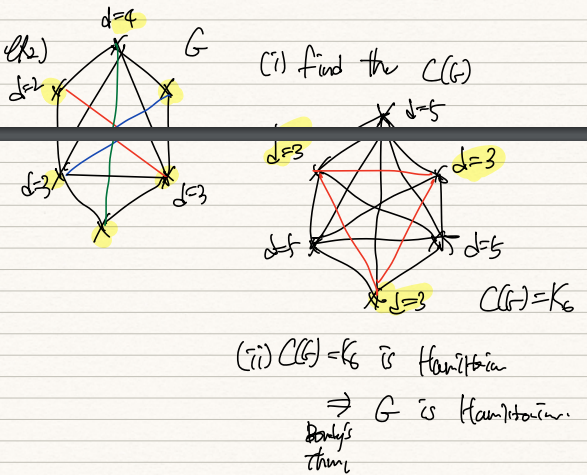





Eulers' Thm) G가 connected라면, G는 Eulerain iff 모든 vertex가 짝수 degree를 가지면
Dirac's Thm) 만약 |V(G)| = n, del(G) >= n/2인 G가 있으면 G는 Hamiltonian이다. 이건 충분조건일뿐...
d = 2 < 3 = 6/2 라서 조건이 충족되지 않았음에도 G는 Hamiltonian이다.
'수학 > 이산수학(Graph Theory)' 카테고리의 다른 글
| [이산수학] (11) Coloring (0) | 2022.06.14 |
|---|---|
| [이산수학] (10) Tree & Spanning Tree (0) | 2022.06.14 |
| [이산수학] (8) Eulrian Graph (0) | 2022.06.13 |
| [이산수학] (7) Connection (0) | 2022.05.18 |
| [이산수학] (6) Subgraphs (0) | 2022.04.20 |



