MAP를 이해하기 위해선 Bayes Theorem을 살펴볼 필요가 있다.
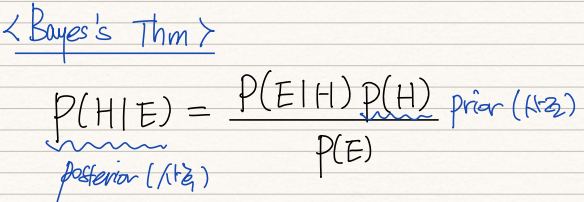
Bayes Thm은 위 식을 의미한다. H는 기존의 Hypothesis를, E는 경험을 통해 획득한 Evidence를 뜻한다. 따라서 P(H)는 prior knowledge를 뜻한다. 반면에 P(H|E)는 Evidence로 sample space를 좁힌 뒤의 P(H) 확률을 뜻한다. 쉽게 풀어말하자면 Evidence를 취득한 뒤의 Posterior probability인 것이다.

Bayesianism의 등장은 확률에 대한 관점의 변화와도 같았다. Frequentism(빈도주의)에 의하면 P(H)=1/2는 100번 동전 던졌을 때 50번 앞면이 나오는 경우로 해석되지만, Bayesian은 동전의 앞면이 나왔다는 주장, 가설의 '신뢰도'가 50%라는 식으로 해석한다. 이들은 확률을 주장,가설의 신뢰도로 인식한다.

해당 관점에서 P(H|E)는 새로운정보인 Evidence를 통해 갱신한 주장의 신뢰도인 것이다. 고로 Bayes Thm은 기존의 신뢰도와 갱신된 신뢰도간의 관계를 식으로 표현한 것임을 알 수 있다.

주사위를 던지는 경우를 가정하면 빈도주의자는 P(Xi)=1/6라는 확률공간을 엄격히 설정하고, 이를 기반으로 실제 관측치가 확률분포에 얼마나 들어맞는지를 확인하는 과정을 통해 유의성을 검정한다.
그러나 Bayesian은 P(X=1)=1/6라는 주장의 신뢰도에 주목한다. 이들은 이 주장의 신뢰도를 실제 관측치를 통해 귀납적으로 갱신하는 과정을 반복하여 실제 P(H)를 찾으려 노력한다.

간단한 예시를 통해 Bayes Thm을 직관적으로 이해해보자. 만약 코로나에 감염될 확률이 전체 인구 대비 0.1%(=P(D))이면, 코로나에 걸린 상황에서 테스트 결과가 양성이 나올 확률은 99%다. 그리고 감염되지 않은 상황에서 음성이 뜰 확률이 98%라고 가정해보자.
이 경우 우리가 실제로 알고 싶은 것은 "내가 양성인데 실제로 코로나에 걸렸을 확률(=P(D|P))이다. 왜냐하면 음성이 나올 경우 P(P|~D)는 2%로 이미 알고 있는 수치고 관심도 없지만, 내가 양성일때 실제로 걸렸는지는 궁금한 사항이기 때문이다.
따라서 posterior prob P(D|P)를 구하기 위해 prior P(D)와의 관계식인 Bayes Thm을 활용한다. 이 때 분모의 P(P)의 확률을 구하는 것이 문제인데, 이는 Law of Total Prob(전확률법칙)을 통해 P를 양분함으로서 쉽게 구할 수 있다.
결론적으로 P(D|P)=4.7%로, 양성이 나왔지만 실제로 코로나에 걸렸을 확률은 4.7%로 극히 낮은 것을 확인할 수 있다. 이는 counter-intuitive한 성질을 갖는데 사람들은 보통 99%의 P(P|D)에 집중하여 0.1%의 P(D)를 신경쓰지 않기 때문이다.
이렇게 갱신된 P(D|P)는 현재 환자가 양성인 event로 Sample Space가 좁혀졌기 때문에 앞으로의 확률계산은 이 P(D|P)=4.7%=P(D)를 기반으로 진행된다. 가령 두번의 일련의 테스트가 모두 양성으로 검출되었을 때, P(D)의 확률을 묻는다면, 두번째 테스트에서의 P(D)는 0.1%가 아닌 4.7%로 갱신되는 것이다.

이러한 기초적 베이스를 갖고 MAP의 원리를 간단한 예시릍 통해 확인해보자.
가령 theta의 확률로 Head가 나오는 동전던지기를 한다고 가정해보자. 이 때 P(D|theta)는 앞서 살펴본 MLE의 likelihood func과 동일하다. 본 예시에서는 pdf가 Bernoulli dist를 따르기 때문에 위와 같은 likelihood func이 대입되었다.
기존 MLE는 likelihood를 극대화하는 theta를 찾아 pdf의 shape과 location을 유추했다면,
MAP는 Bayes Thm을 통해 prior knowledge를 활용하여 posterior probability를 구하고, 이 posterior를 극대화하는 theta를 찾는 방식이다.

분모의 P(D)는 이미 dataset에 의해 확정된 상수와도 같으니 배제한다. 우리는 P(theta|D)의 극대화에 관심이 있으니 P(D|theta)와 P(theta)가 커지면 비례해서 커진다는 사실을 확인할 수 있다.
이 경우 우리는 pdf가 Beta distribution이라고 가정했고, Beta distribution을 따르는 P(theta)를 다음과 같이 전개할 수 있다.
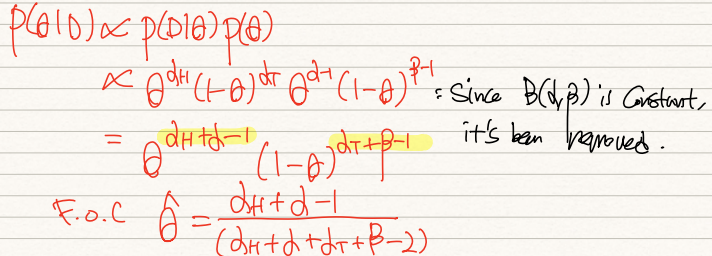
전개한 P(theta)와 P(D|theta)를 곱하여 얻은 값이 위와 같다. 이는 P(D)를 제거했기에 P(theta|D)와 동일한 수식은 아니나, 그와 비례함을 확인할 수 있다. 이 때 양변을 theta로 미분할 경우, estimated theta는 위 식과 같이 도출된다.

theta가 동전이 head가 나올 확률임을 생각했을 때, 이를 직관적으로 해석하면 다음과 같다. 기존의 MLE에서는 (9H,1T)의 dataset이 있다면 theta=9/10이었다. 그러나 이는 우리의 사전지식과 많이 어긋난다. 따라서 이러한 사전지식을 일정부분 포함시켜주는 것이 MAP를 통한 estimation이라 할 수 있겠다.
위 식을 다시 고려해보자. 우리는 이전 실험을 통해 5/10의 확률로 head가 나온다는 것을 prior knowledge로 갖고 있다. 따라서 위식의 alpha=5, beta=5다. 만약 MLE이었다면 9/(9+1)로 끝났겠지만, alpha, beta를 고려한 MAP의 경우 theta가 13/18로 도출된다. 이는 1/2쪽으로 많이 조정된 수치임을 알 수 있다.
그러나 만약 dataset이 2000개와 같이 무수히 많다면 기존의 10회 trial로 형성된 prior knowledge는 영향력을 잃게 된다. 이 경우 실제로 (1800H, 200T)와 같은 결과가 나왔다면 MAP 또한 9/10에 유사한 수치가 도출될 것이다.
마무리짓자면 MAP는 적은 trial로 인한 MLE의 문제점을 prior knowledge를 통해 귀납적으로 갱신해나가며 추정하는 방식이다.
'기계학습 > ML' 카테고리의 다른 글
| [ML개론] (6) Naive Bayesian Classifier (0) | 2022.01.27 |
|---|---|
| [ML개론] (5) Optimal Classification & Bayes Risk (0) | 2022.01.27 |
| [ML개론] (4) Decision Tree & Entropy (0) | 2022.01.26 |
| [ML개론] (3) Rule Based ML overview (0) | 2022.01.11 |
| [ML개론] (1) MLE & Fisher Information (0) | 2022.01.10 |



