기초통계학은 직관에 반하는 불확실성을 계량화하기 위해 존재한다. Data Science field에서의 발전으로 통계학의 중요성이 위축되었으나 그럼에도 불구하고 data가 부족한 경우 통계학은 좋은 tool로써의 역할을 한다.

Sample Space는 실험을 통해 얻을 수 있는 모든 가능사건의 집합이다.
이 Sample Space의 부분집합을 우리는 event라 부른다.

확률에 대해 naive한 정의를 내리자면, 확률이란 모든 가능사건 중 특정 event에 한정되는 사건의 비율을 뜻한다. 즉, Sample Space의 면적 중 부분집합 event A의 면적인 것이다. 가령 동전을 두번 던지는 경우, 4개의 가능사건이 Sample Space 내부에 존재하고, 이중 우리가 <H,H>를 얻게될 확률은 1/4인 것이다.
그러나 해왕성에 생명체가 산다는 experiment의 가능사건이 Yes, No로 양분되지만 P(Yes)=1/2가 아니듯이, <H,H>/ {<H,H>,<H,T>,<T,H>,<T,T>}의 확률이 1/4가 되기 위해선 전제조건이 필요하다. 첫째, 모든 가능사건의 발생확률이 동일해야한다. 우리는 이를 independt & identically distributed(i.i.d)라 부른다. 또한 Sample Space가 유한되어야만 한다.

이제 셈에 대해서 다뤄보자.
경우의 수를 구하기 위해선 multiplication rule이 종종 활용된다. 이는 다자택일을 연쇄적으로 해야하는 상황에서 사용된다. 가령 내가 아이스크림의 맛을 택하고, 아이스크림콘의 종류를 결정한다고 가정해보자. 이 때 나는 3가지의 가능사건(초코, 바닐라, 딸기) 그리고 2가지의 가능사건(와플, 콘)을 연쇄적으로 마주치게 된다. 두 가능사건의 곱이 해당 experiment의 가능사건이다.

그렇다면 이번엔 포커를 칠 때 fullhouse가 나오는 경우를 살펴보자.
우리는 52개의 카드로 구성된 deck에서 5개의 card를 뽑게 된다. 이 때 우리는 combination을 사용하면 된다.
첫째 카드를 선택하는 경우의수는 52, 두번째는 51, ... 이렇게 줄어 52*51*50*49*48의 경우의수가 존재한다. 그러나 이는 뽑는 순서가 반영된 결과다. 예를 들어 내가 처음 뽑을 때 하트킹을 뽑았다면, 그 뒤로는 하트킹을 뽑는 경우가 Sample Space에서 제외된다. 그러나 실제로는 조합된 결과가 중요하지 순서는 combination에서 중요하지 않기 때문에 이를 k!으로 denomite해준다.

full house는 3개의 같은 카드, 2개의 같은 카드로 구성된다. 우선 4개의 다른 문양 중 선택될 3개 혹은 2개를 선택해야하고, 7일지 king일지 queen일지도 결정되어야하니 13 * 4C3 * 12 * 4C2 가 fullhouse가 될 event다. 여기서 13 * 12는 그 순서를 denominate해줄 필요가 없다. '7 3개 & 10 2개'와 '10 3개 & 7 2개'는 완전 다른 것이기 때문에 순서가 중요하다.
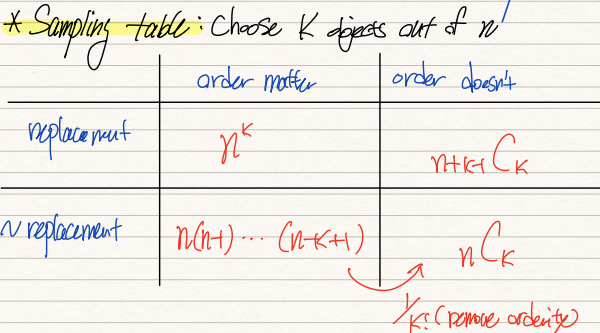
이렇게 선택할 때 순서의 고려여부, 그리고 선택된 것을 다시 복원할지의 여부가 특정 사건의 발생확률을 결정한다.
'수학 > 통계학' 카테고리의 다른 글
| [확률론] (3) Birthday Problem, Properties of Probability (0) | 2022.01.31 |
|---|---|
| [확률론] (2) Story proofs, Axioms of Probability (0) | 2022.01.31 |
| [베이즈통계] (3) 베이즈추정은 정보를 얻을수록 더 정확해진다 (0) | 2022.01.26 |
| [베이즈통계] (2) 방법론의 리스크 vs 선택의 리스크 (0) | 2022.01.26 |
| [베이즈통계] (1) 정보의 획득이 확률을 바꾼다 (0) | 2022.01.26 |



