
위 그림과 같이 SVM이 처리하는 dataset 중 error가 존재하기 마련이다.
이 error를 대처하기 위한 방법은 크게 두가지가 있다. 첫째, error 그 자체의 존재를 인정하되 penalty를 부여함으로서 SVM 모델 간의 성능을 구분한다. 둘째, linear한 decision boundary를 nonlinear하게 변경해준다.
이번 글에선 전자를 살펴볼 계획이다.

penalty는 기존의 min ||w|| 에다가 loss function을 더해줌으로서 부여된다. 더해지는 loss function의 종류에 따라 그 방법이 세분화된다.
첫번째 loss function은 0-1 loss다. Decision Boundary를 넘어서기 전까지 옳은 분류를 하고 있었다면 loss가 0인데, decision boundary를 넘어서는 순간 1로 점프하게 된다. 이 선을 넘는 instance의 갯수를 #_error이고, 갯수에다가 상수값 C를 곱하여 loss function을 더해준다.

그러나 0-1 loss는 그닥 선호되지 않는 것이, boundary로부터 근원에 무관하게 error를 똑같이 적용하기 때문이다. decision boundary 바로 근처에서 발생한 error나 이를 한참 뛰어넘어 발생한 error나 동일하게 count하기 때문에 그리 효과적인 방법은 아니다.

두번째는 hinge loss다. 이는 hinge(경첩)처럼 (wx+b)y < 1인 지점부터 y값인 loss가 linear하게 증가하기 때문에 붙여진 이름이다. 좌측상단의 평면에서 볼수 있듯이 decision boundary와 margin 거리에 위치한 instance의 (wx+b)y 값은 1이 되는데, 이 선으로부터 멀어질수록 loss로 정의된 ε(=(1-(wx+b)y)_+)는 linear하게 증가한다. 이는 해당 지점을 기점으로 (1-(wx+b)y)가 양의 영역으로 접어들기 때문이다.

이 ε를 slack variable이라 부른다.
이 slack variable ε를 모두 더하여 상수 C를 곱한 값이 loss function이 된다. 우리는 ||w|| + loss fn 을 최소화해야하는데 이를 soft margin이라 부른다. 이 때 C를 잘선택해야 절저하게 최적화된다.

마지막은 log loss다. linear하게 error를 처리했던 hinge loss와는 달리 margin distance보다 멀리 있는 instance에도 penalty를 부여하고, decision boundary를 벗어난 instance에 대해서도 boundary로부터 많이 벗어날수록 그에 가중되는 penalty를 부여하는 함수다.

이 log loss는 logistic regression에서 비롯되었다. 두번째 줄을 보면 YX(theta)가 마치 (wx+b)y의 형태와 유사하며, 뒷부분의 log항은 마치 loss function처럼 기능하는 것을 확인할 수 있다. 따라서 우린 이 log항에 YX(theta) (이경우 (wx+b)y)를 대입하여 log loss fn의 slack variable로 활용한다.
사실 세함수 중 우월을 가리기는 힘들다. 각자의 모형에 맞는 loss fn을 활용하면 좋다.
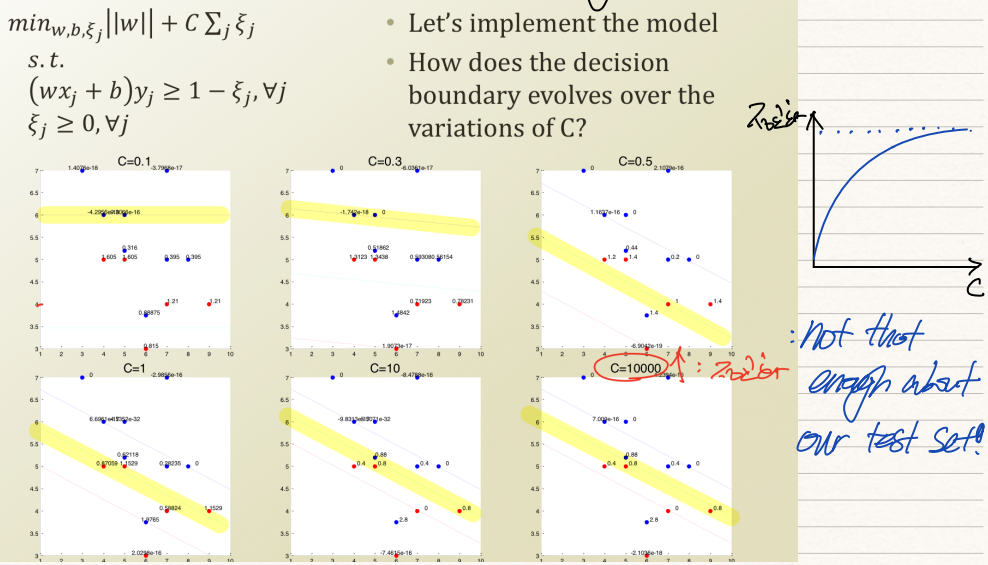
그렇다면 마지막으로 어떠한 C를 사용해야하는가? C는 penalty의 강도를 뜻한다는 점에서 모델의 정교함과 비례한다.
위 예시처럼 c=0.1일때보단 c=1일때가, c=1일때보단 c=10000일때가 모형의 정교도가 높다.
그러나 c를 무작정 높게 잡는 것은 상당히 위험한 일이다. 우리가 갖고 있는 training set이 되게 편향된 data일수도 있기 때문에 미래에 '편향되지 않은' data가 입력될 경우 이 data에 대한 분류를 엉망으로 진행할 가능성이 크다.
'기계학습 > ML' 카테고리의 다른 글
| [ML개론] (13) dual problem of SVM (0) | 2022.02.21 |
|---|---|
| [ML개론] (10) Naive Bayes to Logistic Regression (0) | 2022.02.20 |
| [ML개론] (11) Support Vector Machine(SVM) (0) | 2022.02.04 |
| [ML개론] (9) Gradient Method for Regression (0) | 2022.02.02 |
| [ML개론] (8) Gradient Method (0) | 2022.02.02 |



