
A가 nonsymmetric한 경우를 방지하기 위해 symmetric rank-one update가 도입된다. 이는 u*v에서 u*u로 broyden's method의 단점이 보완된 형태다.
Hk+1 = Hk + u*u의 양변에 yk를 곱한다. Hk = inverse of (yk / sk) 이기 때문에 Hk*yk는 sk가 된다. 이 식을 정리해주면 우측 상단의 식이 전개된다. u*u*x를 (u*u) * x가 아닌 u*(u*x)로 본다면 괄호 안의 항은 scalar의 형태가 된다. 그럼 이 식은 vector u에다가 특정 scalar값을 곱해주면 z가 된다는 뜻이 된다.
그러면 u는 z와 무조건 평행한 일직선상 위에 놓여야하며 u*x는 무조건 특정한 값이어야만 한다. 따라서 x와 z값만 알고 있다면 u는 u혹은 -u라는 유이한 solution으로 결정된다.
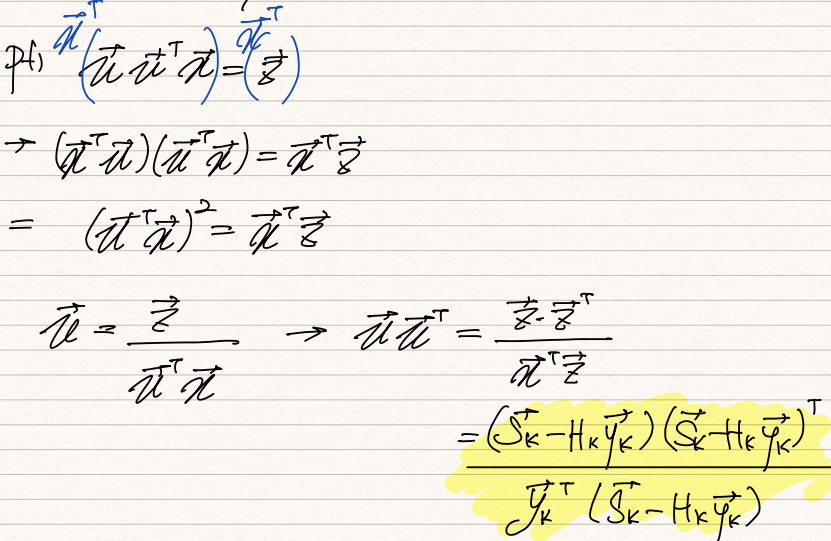
SR1 mtx를 구하기 위해 transpose of x를 양변에 곱하면 위와 같이 전개된다.

정리를 하자면 우린 여전히 원함수의 local min을 찾고 싶은데, 이를 quasi newton의 개념 아래 진행하고 싶다.
Bk를 사용하는 quasi newton 대신 그 inverse인 Hk 관게식을 구해 계산의 복잡성을 줄인 broyden's method를 사용하려 했다. 그런데 이 방법은 Hk가 symmetric이 안될 수 있다는 치명적 단점이 존재하여 SR1 update를 활용하게 되었다.
우린 Xk+1 = Xk - Hk*f(xk)은 f(x*)=0이 되는 x*를 찾기 위한 식이고, 이 Hk를 간편히 구하기 위한 관계식이 두번째 식이다. 우변의 뒷항은 Symmetric rank-one mtx이다.
알고리즘은 다음과 같이 전개된다.
주어진 시점 x0을 통해 f(x0)을 구한다. x_-1은 없기에 hessian mtx를 통해 H0을 구한다.
그럼 위 그림의 첫째 수식을 통해 x1을 구할 수 있고, 똑같은 작업을 f(x*) = 0 이 되는 x*를 찾을 때까지 반복한다.

그러나 SR1 update에도 단점은 존재한다. 첫째, SR1의 분모가 0에 수렴할 경우 행렬이 매우 큰 숫자가 도출되어 문제를 해결할 수 없게된다. 둘째, Hk+1이 positive definite라는 사실을 보장할 수 없다. positive definite에 대한 설명은 SR1의 보완책인 BFGS와 DFP를 설명하면서 진행하겠다.
'기계학습 > Optimization' 카테고리의 다른 글
| [최적화] (8) Infeasible Start Newton's Method (0) | 2022.02.21 |
|---|---|
| [최적화] (7) Lagrangian Multiplier Method (0) | 2022.02.21 |
| [최적화] (4) Broyden's Method (0) | 2022.02.05 |
| [최적화] (3) quasi Newton Method (0) | 2022.02.05 |
| [최적화] (0) scalar를 vector로 미분 (0) | 2022.02.04 |



