
이전 글에서 testing을 하는 이유와 그 방법론에 대해 알아봤다. 그럼 testing의 결과는 어떻게 측정되는가?
사실 true fn과 average hypothesis를 통해서 bias와 var를 구하는 것이 가장 좋지만 이들은 계산불가하다.
따라서 우리는 performance mtx를 활용하여 error를 측정하고자 한다.
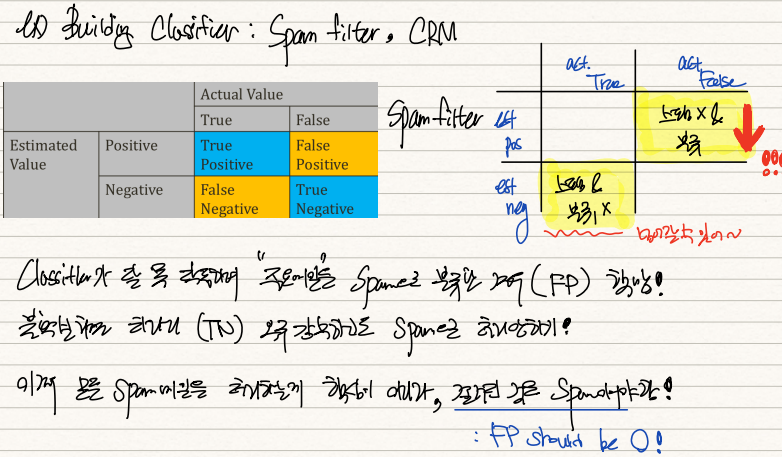
만약 우리가 classifier로 스팸필터를 설계했다고 가정해보자. 스팸필터의 핵심은 "스팸이 아닌 메일을 스팸으로 분류하면 안된다"는 것이다. 스팸메일을 일반메일로 분류하면 그냥 삭제해주면 되지만 일반메일인데 스팸메일함에 들어가 있으면 이를 놓치게 되기 때문이다. 따라서 우리는 False-positive, 즉 스팸이 아닌데 스팸이라고 판독한 1종오류를 중점적으로 측정해야한다.

스팸필터의 성능을 측정하기 위해서 Precision rate를 사용한다. 이는 TP/(TP+FP)로 계산된다. TP는 True-positive로 실제스팸메일을 스팸메일로 처리하는 경우이고, FP는 일반메일을 스팸메일로 처리하는 경우다. 우리는 FP의 case가 0이길 바라니까 Precision rate가 높으면 높을수록 좋다. 이 경우 Recall rate는 높으면 좋지만 낮아도 괜찮다.
다른 예시로 백화점 고객명부 10,000명 중 VIP고객을 골라내는 classifer, CRM이 있다고 가정하자.
VIP는 10,000명 중 10명 정도로 극소수이기 때문에 그들을 놓쳐서는 안된다. 즉 VIP가 아닌 사람들에게 promotion 전단지를 실수로 발송하더라도 VIP에게 전단지를 발송하지 못하면 안되는 것이다. 이 경우엔 True-Negative, 즉 VIP인데 VIP가 아니라 판단하는 error인 2종오류를 줄여야한다.
이 CRM의 기능을 측정하기 위해선 Recall rate를 사용한다. 이는 TP/(TP+FN)인데 FN이 VIP를 VIP라 판단하지 않는 오류이기 때문에 CRM의 기능이 좋으려면 Recall rate가 높아야 한다. 이 경우 Precision rate는 높으면 좋지만 낮아도 괜찮다.

F-measure는 Precision rate와 Recall rate을 동시에 반영한 값이다. 이는 rate에 weight인 b을 가중부여하여 계산한 값이다. 가령 b=1인 F-1 measure의 경우 두 rate가 동일하게 반영된다. b=2이면 recall rate에 가중치가 부여되고, b=0.5면 precision rate에 가중치가 부여된다. F-measure는 precision, recall rate보다 더욱 빈번하게 사용되고 있다.

그러면 이제 complex model을 regularization(정규화)하여 complexity에 의한 error, 즉 variance를 줄여보자.
위 예시를 살펴보면 0.1, 0.2 부근의 관측치 2개에 의해 g1모형이 엉뚱하게 형성된 것을 알 수 있다. 이는 variance가 매우 커지는 결과로 이어진다. 그렇다고 variance를 줄이기 위해 우리가 저차모형인 constant를 선택하는 것은 좀 애매하다. constant line은 예측능력이 많이 떨어지기 때문이다.
이 때 우리는 sampling이 이상하게 되었을 때 발생할지도 모르는 높은 variance를 사전에 줄이기 위해 regularization을 활용한다. 이를 통해 우리는 training dataset에 대한 accuracy를 다소 줄이고 앞으로 들어올 dataset에 대한 potential fitness를 높인다.

SVM을 설계할 때 우리는 Kernel의 차수를 높이면서 모형을 더욱 복잡하게 만들 수 있었다. 그러나 이는 training dataset에 과적합될 수 있으며 bias 또한 높아진다. Regularization은 regression에 대한 새로운 제약조건과도 같다.
가령 g모형의 weight를 학습시켜 training dataset에 대한 squared error를 줄이려고 한다고 가정해보자. 이 경우 우리는 weight를 training dataset에 overfitting시킬 위험에 노출된다. 따라서 regularization term을 기존 MSE term에 더하여 학습을 진행한다. Ridge regression의 경우엔 lambda*(1/2)*||w||^2를, Lasso regression의 경우엔 lambda*|w|을 더한다.
이렇게 cost function에 regression term을 더하는 행위 자체가 MSE term에 constraint를 더하는 것이다. Ridge의 경우 위 그림을 살펴보면, contour의 한 가운데에 constraint없이 최적화한 beta값이 위치한다. 그런데 이 beta값이 지나치게 우리의 dataset에 overfitting되었을 수 있기 때문에 우리가 제약을 걸어준다. L2 norm의 값에 대한 제약이니 원점을 중심으로한 원과 맞닿은 지점이 regularized weight가 된다.


MSE+reg.term을 w에 대해 미분해주면 위와 같이 전개된다. 결국 W=X^{T}*Y*(X^{T}*X+lambda*I)^(-1)으로 도출된다. 이는 least square의 closed form에 labmda*I를 더해준값이다. 따라서 lambda의 값이 크다면, 즉 cost function에서 regression term의 영향력이 크다면 weight는 작아져서 원점에 가까워질 것이다. 반면 labmda의 값이 작다면 weight값은 커져서 원래 MSE로 구한 beta값에 가까워질 것이다.

위 예시는 lambda=1로 regularization한 것이다. variance가 상당히 높았던 기존 모형과는 달리 reg.term이 추가됨에 따라 bias는 살짝 높아졌으나 variance는 크게 낮아졌다. regularization의 핵심적인 성취는 complexity를 유지하면서, 즉 bias를 크게 낮추지 않고 variance를 낮췄다는 것이다.
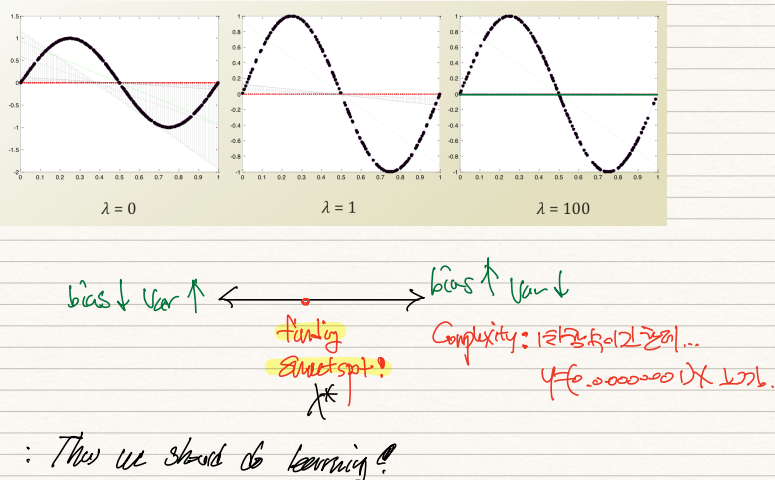
이는 lambda값을 좌측부터 0, 1, 100으로 설정했을 때의 모형변화다.
상술했듯이 lambda=0이면 MSE를 통해 구한 weight와 똑같은 값이 출력되어 variance가 높고, lambda=100이면 reg.term이 지나치게 큰 영향력을 갖게되어 weight=0에 수렴하게 된다. 이 경우 variance는 낮아지지만 사실상 0차나 다름없는 1차함수이기 때문에 bias가 높아진다. 따라서 우리는 양 극단 사이의 sweetspot을 찾아서 학습시켜야한다.

LR에도 regularization term이 추가될 수 있다. 그러나 closed from의 형태로 theta값이 딱 떨어지는 linear regression과는 달리 LR은 gradient descent method를 활용해야한다. 따라서 이 부분을 알맞게 조정해주면 된다.

SVM에서도 regularization 기법이 활용된다. soft margin 개념이 그 것이다. soft margin을 다룰 때 C의 크기에 따라 모형의 overfitting, underfitting이 결정되는 것을 확인했다. C를 매우 크게하면 penalty를 지나치게 많이 주는 것이 되어 모형이 과적합되는 반면, C를 낮추면 penalty가 덜 반영되어 모형이 단조로워진다. 이러한 특성이 L1, L2 regularization의 그것과 유사하다. 따라서 SVM의 soft margin은 regularization의 special case라 인식한다.
'기계학습 > ML' 카테고리의 다른 글
| [ML개론] (19) Bayesian Network (0) | 2022.02.25 |
|---|---|
| [ML개론] (18) Review on Probability (0) | 2022.02.25 |
| [ML개론] (16) Occam's Razor & N-fold cross validation (0) | 2022.02.24 |
| [ML개론] (15) bias & variance (0) | 2022.02.24 |
| [ML개론] (14) dual SVM with Kernel (0) | 2022.02.21 |



