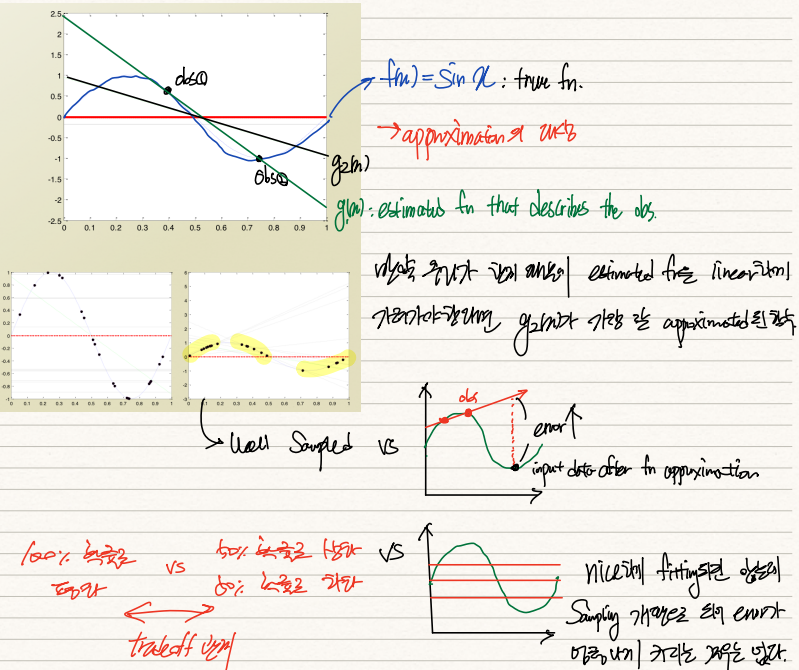
우리는 dataset을 활용하여 g(x)를 학습시키려고 한다. 이 g(x) 함수는 true fn인 f(x)=sin x를 예측하는 것이 그 목적이다.
실제 dataset은 sin x를 따르고 있는데, 우리에게 주어진 관측치가 두 점 밖에 없을 경우 우리는 녹색선으로 목표함수를 예측할 것이다. 그러나 이는 sin함수를 잘 설명하지 못한다.
비슷한 예로 관측치가 sin함수 봉우리 상단에 몰려있다고 가정하자. 그럼 해당 관측치를 기반으로 예측된 목표함수는 우상향하는 직선이 될 것이다. 그러나 이 경우 실제로는 봉우리 하단에 위치할 값과의 오차가 극대화된다.
반면 이번에는 수평선을 그어 목표함수를 예측하는 경우를 생각해보자. 이 경우 이전 예시와는 달리 큰 error가 발생하진 않을 것이다. 그러나 모형이 지나치게 단조롭기 때문에 대부분의 값에 있어 오차가 일정정도 발생하게 된다.
이처럼 모형의 복잡도(차수)에 따라 error의 발생빈도, 그 폭이 상이하다. 차수가 낮으면 error는 더 자주, 적게 발생하는 반면, 차수가 높으면 error가 가끔, 더 심하게 발생한다.

위 그림은 차수별로 bias와 variance를 구한 결과다. 실제로는 true fn을 모르기에 이 값들을 구할 순 없으나 이 경우 true fn을 sin함수로 지정했기 때문에 계산가능하다. 또한 average hypothesis를 구하였고 그 g bar 모형이 위 그림 상 파란선으로 표시되어있다.
좌측의 simple model은 정밀하게 예측하는 능력이 떨어져 data에 대한 bias가 다소 높은 반면 분산값은 매우 작다.
우측의 complex model은 정밀하게 예측할 때는 예측하지만 그렇지 못할 때는 심하게 틀리기 때문에 bias는 작은 반면 분산값은 높다. ML model을 설계하는 과정에 있어 우리는 bias와 variance간의 tradeoff에 집중해야한다.
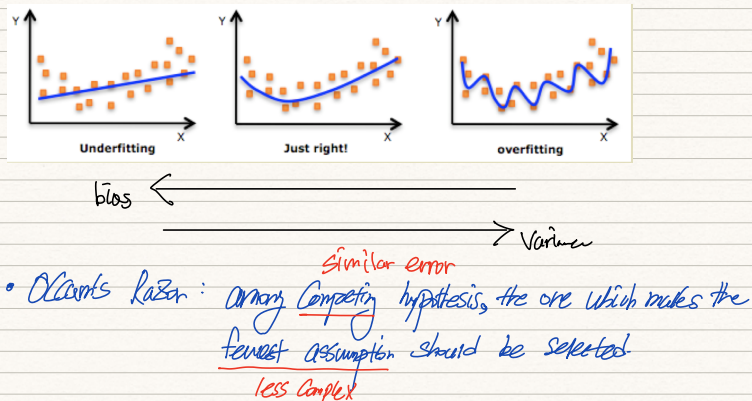
위 그림을 살피면 우측의 모델은 bias가 극소화되어있지만, 분산은 높고 좌측 모델은 분산값은 작지만 bias는 높다.
만약 특정 모형 2개의 error값이 차이나지 않는다면 우리는 가장 가정이 덜 들어간, 즉 simple한 모형을 선택해야한다. 이 경우 추후 처리할 input data를 더 잘 handling할 수 있기 때문이다.

여지껏 true fn을 안다고 가정하고 bias와 variance를 측정했다. 그러나 현실에선 이 두 수치를 측정할 수 없을 뿐더러 data를 무한히 sampling하여 g bar 모형을 만들 수도 없다.
따라서 우린 Cross Validation(CV)를 통해 유사 infinite sampling을 시행한다. 가령 우리가 10,000개의 data를 갖고 있다면 이를 동일한 data를 내재하는 N개의 부분집합으로 나눈다. N-1개의 부분집합은 training에 활용하고 나머지 1개의 집합을 testing으로 활용한다. 이러한 과정을 N번 반복한다면 infinitely many sampling를 통해 average hypothesis를 추정하던 것과 유사한 결과를 얻을 수 있게 된다.
K-fold CV의 극단적인 케이스는 LOOCV인데 이는 단 한개의 instance를 test set으로 지정하고 모든 데이터에 대해 CV를 진행하는 것이다.
'기계학습 > ML' 카테고리의 다른 글
| [ML개론] (18) Review on Probability (0) | 2022.02.25 |
|---|---|
| [ML개론] (17) F-measure & Regularization (0) | 2022.02.25 |
| [ML개론] (15) bias & variance (0) | 2022.02.24 |
| [ML개론] (14) dual SVM with Kernel (0) | 2022.02.21 |
| [ML개론] (13) dual problem of SVM (0) | 2022.02.21 |



