앞서 Ch.7에서 하나의 설명변수로 종속변수를 설명하는 simple regression에서 벗어나 2개 이상의 설명변수를 활용하는 multiple regression model을 살펴봤다. Ch.8에서는 multiple regression의 함정을 살펴 이를 보완할 방법을 공부한다.

모형을 정교화할 때 살펴봐야할 사안들은 다음과 같다.
첫째, 종속변수를 설명함에 있어 특정 독립변수를 삽입하는 것과 방출하는 것 중 어느 것이 효과적인가?
둘째, 종속변수를 설명함에 있어 특정 독립변수의 형태는 선형이 효과적인가, 비선형(log, 제곱 등)이 효과적인가?
셋째, 데이터를 측정하는 과정에 있어서 오차가 발생하진 않았는가?
넷째, 표본의 분포가 정규성을 따른다는 가정이 그릇되진 않았는가?
다섯째, 설명변수와 잔차간의 유의미한 상관성이 존재하는 내생성문제가 있진 않은가?
1. Model & Assumptions

2. Inclusion vs Omission of variables?

모형의 설명력을 높이기 위해 변수를 삽입하거나 방출하는 절차를 밟아야 한다. 이 때 두가지의 오류가 발생할 수 있다.
첫째, 모형의 설명력을 높이는데 도움되지 않는 변수를 삽입한 경우, 즉 1종오류(Type I error)의 발생이다.
둘째, 모형의 설명력을 높이는데 도움되는 변수를 방출하는 경우, 즉 2종오류(Type II error)의 발생이다.
1) Omission of relevant variables(β3!=0)

유의미한 회귀계수 β3를 0이라고 오판하여 설명변수 Z를 방출한 경우다.
이 때 오판하여 새로이 설정된 assumed model이 존재하고 이를 표본을 통해 추정한 estimated model이 존재한다.
이 때 회귀계수 β2는 여전히 BLUE(best linear unbiased estimates)인지 확인해보자.

우선 불편추정량인지부터 확인해보자.
만약 불편추정량이면 모회귀계수 β2를 추정한 값인 b2*의 평균값 역시 β2가 되야한다. 그러나 이 경우 실제모형의 E(yi)가 β1+β2Xi+β3Zi이기 때문에 이를 대입하면 β2+β3Γ가 도출된다. 이 때의 β3Γ는 방출된 변수 Z에 의한 bias를 나타낸다. 위 식을 통해 Sxz/Sx^2가 Γ를 나타내는 것을 확인했기 때문에, Γ는 결국 Z에 대한 X의 회귀계수임을 알 수 있다.
Ch.7에서 살펴봤던 total effect와 이를 연결시켜보면 이해가 쉽다.
실제모형의 SRF는 yi=b1+b2Xi+b3Zi+ei이며, X의 변화가 Y의 변화로 이어지는 정도를 파악하기 위해선 total derivatives를 활용할 수 있다. 이 때 결과는 E(b2*)=β2+β3(∂Z/∂X)가 도출됨을 우리는 안다. 따라서 True model과 assumed model간의 괴리가 있는 상황에선 편향이 발생할 수 밖에 없다.
물론 ∂Z/∂X가 0이면 두번째 항이 0이 되면서 편향이 사라질 수는 있겠으나, 이는 Z 설명변수가 회귀식에 존재한다는 가정 하에 X와 Z간의 공분산이 0임을 뜻하기 때문에 "설명변수간의 완전선형성이 존재하지 않는다"는 대전제에 위배된다.

과녁의 중앙에 도달하지 못하더라도, 탄착점이 모여있으면 좋은 추정치가 될 수 있다.
그러나 애시당초 E(b2)!=β2기 때문에 전제가 흐트러진다. 이 경우 error term이 영향을 받기 때문에 t-test를 할 수 없게 된다. 따라서 sample을 활용한 모분산에 대한 추정 그 자체가 불가능하기 때문에 t-test가 불가한 것이다.

만약 X, Z 설명변수 간의 선형관계가 없는 경우, 둘간의 공분산은 0이 되어 bias가 없어진다.
공분산이 0이란 것은, indirect effect가 없다는 것을 뜻하기 때문에 둘 중 하나의 변수를 방출해도 total effect는 손해보는 것이 없어진다. 그럼에도 불구하고, 오차항의 분산에 대한 추정과 b2 분산에 대한 추정량에 편의가 발생하게 되어 t-test는 못한다.
2) Inclusion of irrelevant variables(β3=0)

이번에는 무의미한 설명변수, 즉 β3=0인데 이를 회귀식에 포함하는 경우를 살펴보자. 우리는 이를 1종오류라 부른다.

이전과 같이 식에 대입하는 E(b2)를 구해주면 실제 True model의 E(yi)가 β1+β2Xi이기 떄문에 E(b2)=β2가 도출된다.
LS estimator b2에 편향이 존재하지 않음을 뜻한다.
그렇다면 탄착점이 중앙에 위치함은 알겠는데, 이들이 과도히 분산되어있진 않은가를 확인해줘야한다.
다행히 b2의 평균값이 불편추정량이기 때문에 t-test는 할 수 있다. 상관계수가 0이 아니라는 가정 하에, V(b2)가 V(b2*)보다 당연히 크다. 따라서 inefficient하다.

이 때 X와 Z간의 상관성이 높아질수록 분산은 커지기 때문에 b2 estimate에 대한 t-ratio는 감소한다.
즉, 어차피 Z가 Y의 변화량 설명에 그닥 효율적이지 못한 변수인데, 심지어 X와 그 선형적 상관성마저 높다면 있어야할 필요가 없다는 것이다.
3) Decision : Mean Square Error(MSE)

sum up하자면, β3가 쓸모있는데 버리는 경우엔 bias가 발생하지만 variance는 어느정도 잡히는 반면, β3가 쓸모없는데 넣으면 bias는 발생하지 않지만 variance는 높아진다.
따라서 우리는 MSE를 도입하여 β3에 상응하는 설명변수를 포함시킬지 말지를 결정할 수 있다. True model 뭔지를 모른다고 가정하면 β3를 누락하는 경우에는 편의가 발생할 가능성이 있고, β3를 포함하는 경우에는 variance가 높아질 가능성이 있다. 따라서 variance와 bias에 대응하는 항을 분리하여 이둘을 비교한다.


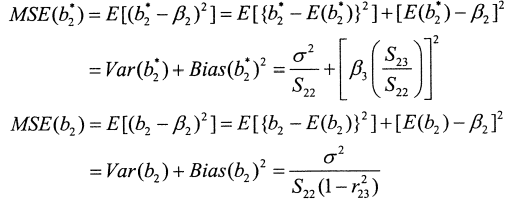
MSE 값의 변동을 일으키는 변수는 결국 x,z간 상관계수(Γxz)와 β3의 절대값이다.


만약 β3의 절대값이 커진다면, 즉 해당 설명변수의 설명력이 커지면 이를 누락하는 것이 오류다. 따라서 2종오류를 범한 MSE(b2*)의 값이 커지기 때문에 해당 변수를 포함한 b2를 선호하게 된다. 이 경우 2종오류가 아닌 잠재적 1종오류를 저지르는게 낫다는 판단을 내린다.
만약 Γxz의 절대값이 커진다면, 즉 설명변수간의 선형적 상관성이 높아지면 이를 포함하는 것이 오류다. 따라서 1종오류를 범한 MSE(b2)의 값이 커지기 때문에 해당 변수를 누락한 b2*를 선호하게 된다. 이 경우 1종오류가 아닌 잠재적 2종오류를 저지르는게 낫다는 판단을 내린다.
'계량경제학 > 계량경제학' 카테고리의 다른 글
| [계량경제학] 12. autocorrelation (0) | 2021.12.14 |
|---|---|
| [계량경제학] 11. Heteroscedasticity (0) | 2021.12.09 |
| [계량경제학] 9. multiocollinearity (0) | 2021.12.08 |
| [계량경제학] 10. Dummy Variable Model (0) | 2021.12.08 |
| [계량경제학] 7. multiple regression model (0) | 2021.12.08 |



