1. sources, Nature of Autocorrelation
1) Inertia

자기상관이란 주로 시계열데이터에서 많이 관측되는 특성이다. 예를 들어, GDP, 수출입지표, 고용지표 등 이전 관측자료가 다음 관측치에 큰 영향력을 행사하는 데이터에서 많이 발견된다. 간단히 생각해보면 98년도 외환위기가 이후 수십년간 한국경제에 큰 영향을 미쳤기 때문에 해당년도의 변화가 계속 영향력을 행사한다.
이 경우 t시기의 error term과 s시기의 error term간에 공분산이 0이 아니게 되어 여지껏 살펴봤던 Gauss-Markov Thm의 핵심가정이 흔들리게 된다. 이렇게 되면 자연스레 t-test 등 여지껏 해왔던 것들을 할 수 없게 된다.
2) Specification bias: excluded variables

이렇게 자기상관이 발생하는 경우는 크게 5가지 경우가 존재한다.
첫째로 model에서 제외된 변수에 의한 자기상관이다. 예를 들어서 KOSPI 주가지수를 종속변수로 설정했을 때, 이를 설명하는 변수로 환율만 놔두면 기업의 영업이익과 같은 빠진 변수에 의한 자기상관이 발생한다. 여기서 말하는 자기상관이란, 항상 오차항끼리의 자기상관을 뜻하는 것을 명심해야한다.
따라서 이런 경우엔 그저 영업이익을 설명변수로 새로 추가하면 문제가 어느정도 해결된다.
3) Specification bias: incorrect func form

두번째로는 잘못된 함수모형이다. 설명변수가 종속변수에 nonlinear한 영향을 행사하는데 이를 무시하고 linear하게 모형을 구성했다면 그만큼 오차가 발생하기 마련이다. 위 경우 음영만큼의 error term이 발생했고 이는 단순히 random한 오차가 아니라 trend를 따르기 때문에 자기상관이 발생한 것이다. 따라서 nonlinear하게 만들어주면 해결된다.
4) Lagged variable model

세번째는 이전과는 다르게 전 관측기의 종속변수 데이터가 그 다음 관측기의 종속변수에 영향을 미치는 경우다.
이는 관습적이거나 심리적, 기술적, 교육 등의 요인에 의거해 발생한다. 예를 들어 삼성전자 주가가 오늘 10만원인데 내일 3만원으로 당장 내려갈 수 없는 이유는 상/하한가 제도가 도입되어있다는 institutional한 이유 때문이다.
이 경우 만약 우리가 Yt-1을 무시한다면 이는 error term에 포함될 것이고, 오차항은 자기상관성이 높아질 것이다.
5) Data tranformation

네번째는 데이터를 변환하는 과정에서 발생하는 자기상관 이슈다.
위와 같이 t년도 데이터에서 t-1년도 데이터를 빼서 변화량을 알아보는 경우, 새로이 생성된 회귀식에서 error term이 겹치는 자기상관 현상이 발생하곤 한다.
아래의 nonstationary 관련해서는 unit root, ADF test에 대해 따로 정리해 업로드할 계획이다.
2. Problems of Least Squares Estimator under Autocorrelation


자기상관이 발생하는 경우엔 이전 공분산의 경우와 마찬가지로, LS estimator가 과녁 가운데에 평균적으로 꽂힌다. 그러나 그 분산의 정도가 최적화되진 못해있다. 이는 이전엔 공분산=0으로 처리해왔으나 이젠 0이 아니기 때문이다. 따라서 OLS를 사용하지 못하고 이전 공분산때처럼 똑같이 특수한 작업을 거쳐야 한다.

3. Typical Type of autocorrelation: AR(1)

위에서 살펴봤듯이 자기상관이 발생할 수 있는 여러 상황이 존재하나, 학부 수준에서는 AR(1) 모형을 기초로 설정한다.
AR(1) 모형은 Et와 Et-1간의 자기상관성이 존재한다고 가정하며, 위의 식을 통해 이들의 관계를 설정한다. 이 때 Et와 Et-1간의 관계에서도 error term이 존재하는데 이를 white noise라 부르며 기존 Gauss-Markov Thm의 가정을 따르는 오차항이라고 가정한다.



비록 error term간의 자기상관이 존재하지만 위의 식을 통해 error term의 평균은 우선 0이며, 분산은 무한등비급수를 따르는 white noise의 분산임을 확인할 수 있다. 또한 자기상관이 없을 때의 공분산이 0인 error term과는 달리, 자기상관이 있는 경우 시차를 둔 error term간의 공분산은 0 이상임을 확인할 수 있다.
이에 따라 당연히 error term간의 상관계수 또한 존재한다.

t와 t+s간의 상관계수는 P^s로 결정된다. 이 때 p가 1보다 작아 0으로 무한히 수렴한다고 하더라도, t시점의 error term의 변화가 exponential하게 t+s시점의 error term의 변화로 이어지게 된다.

만약 절대값 p가 1이라면 어떻게 될까? 앞서 언급했던 nonstationary 상황이 된다.
error term의 분산이 무한으로 발산하기 때문에 정신없이 아무렇게나 움직이는 random-walk가 구현된다.
4. detecting autocorrelation
1) Graphical Method

자기상관을 우선 감지하고 이를 보완하여 기존의 OLS를 사용한다.
우선적으로 그래프를 통해 시각적으로 자기상관의 존재를 파악하는 방법이 있다. Et에 대해 설명변수 Et-1이 p의 계수를 가져 둘이 유의미한 패턴을 보인다면 자기상관이 있는 것이다.
2) Durbin-Watson Test

가장 많이 사용되는 방식이다. 기존 AR(1) 모형에서 Et와 Et-1에 대해 위와 같이 OLS를 돌린다.
만약 이 때 귀무가설, 상관계수 ρ=0이 기각되면 Et와 Et-1간의 자기상관이 없다는 것으로 판정난다.

그렇다면 왜 d를 사용하는지에 대해서 살펴보겠다.
식을 풀어보면 Sum of Et^2과 (Et-1)^2이 존재하는데 이들은 E1^2만큼 차이가 나는것이니 같은 것으로 간주한다. 따라서 이를 분모의 SUm of Et^2로 나눠주면 2가되고, 뒤의항은 분모로 나눠줄 경우 corr(Et,Et-1)=ρ가 도출된다. 이것도 곰곰히 생각해봐야하는데, 이전에 Sum of Et^2와 Sum of Et-1^2을 같은 것으로 간주했으니 분모를 Et와 Et-1의 표준편차로 풀어볼 수 있다. 분자는 여전히 E의 평균은 0이기 때문에 Et와 Et-1의 공분산이다. 따라서 d=2(1-ρ)이 도출된다.
상관계수 ρ가 -1과 1 사이에 존재하기 때문에 d는 0과 4 사이에서 존재한다.
만약 ρ hat이 0이면 d는 2, 1이면 d는 0, -1이면 d는 4가 도출된다. 다소 복잡한 면이 없잖아 있다.


decision reule은 위와 같다.
a. d < dL : reject H0
b. dL < d < dU : no decision
c. dU < d < 4-dU : do not reject H0
d. 4-dU < d < 4-dL : no decision
e. 4-dL < d : reject H0
d가 0과 4 사이에 위치한다는 점에서, dL보다 작으면 이는 d가 0에 가까운 것이고, 즉 ρ가 거의 1임을 알 수 있다.
반대로 4-dL보다 d가 큰 경우엔 ρ가 거의 -1에 가까워 음의 상관관계를 가진다. 반면 dU < d < 4-dU의 경우엔 ρ가 중간에 위치하니 ρ가 0에 가까워 가설을 기각하지 않는다.
사실 이와 같이 No decision을 만드는 이유는 편의를 위함이다. 가설을 기각하기 위한 신뢰구간 95%가 분명 DW test에도 존재한다. 그러나 d*가 array X에 의존하여 도출과정이 꽤나 복잡하기 때문에 dL, dU를 사용한다. 이는 정확히 d* 값은 아니지만 그보다 좀 더 robust한 값이라 이를 채택한다. 이렇게 되면 dL과 d* 사이 구간은 95% 신뢰구간을 벗어나 H0 기각조건을 충족함에도 불구하고 N.D 구간이라 무시된다.

DW test를 위해선
a. regression model에 intercept term이 포함되어야한다.
b. AR(1) model을 검증하는데 효과적이다.
c. 분기별 데이터는 변형된 AR(4)형태이기 때문에 b 조건과 배치된다. 따라서 DW-test가 적합하지않다.
d. Lagged dependent variable이 존재하면 DW-test가 불가하다.
3) Lagrange Multiplier Test(Breusch-Godfrey Test)

DW test의 약점인 Lagged dep. variable을 다루지 못하는 것을 보완하기 위해 LM test를 실시한다. 이는 카이제곱분포을 사용하여 정확한 신뢰구간 범위를 기반으로 test를 돌릴 수 있고, lagged model을 다룰 수 있다는 장점이 있다.
a. LS of Yt on (Xt, Yt-1, 1)를 돌리고 잔차항을 구한다.
b. LS of et on (1, Xt, et-1)를 돌리고 결정계수를 구한다.
c. 만약 et-1과 et간의 상관계수가 0이라면 결정계수가 낮을 것이고, 0이 아니라면 높을 것이다.
d. LM = nR^2이 카이제곱분포(1)을 따르기 때문에 LM>카이분포값을 넘기면 가설을 기각한다. 즉, et와 et-1간의 자기상관은 존재한다.
5. Remedy for autocorrelation
1) GLS(when ρ is known)

만약 ρ가 알려져있는 경우를 가정하면,
a. ρ를 Yt-1 회귀식의 양변에 곱해 이를 Yt식에 빼주면 된다. 이러면 error term식에 white noise밖에 남지 않아 자기상관이 사라지게 된다.
b. LS of Yt*(=Yt-ρYt-1) on (1, Xt*)을 구하면 된다. 이는 자기상관이 제거된 데이터라 OLS로 작동한다.

이런 GLS의 작업은 차감해준 ρYt-1의 항을 우변으로 넘겨줄 경우 f(Xt, Xt-1, Yt-1) + ut의 lagged dependent variable 모형으로 정리할 수 있으며 이는 자기상관을 없애준다.
2) FGLS(when ρ is unknown)

이번엔 상관계수를 모르는 FGLS의 경우다.
a. LS of Yt on (1, Xt)를 돌리고 잔차항을 구한다.
b. LS of et on (et-1)을 돌리고 ρ의 추정치를 구한다.
c. 이전과 같이 ρYt-1을 Yt에 빼주어 Yt*을, Xt*=Xt-ρXt-1을 해주어 식을 만들고
d. LS of Yt* on (1, Xt*)을 해주면 된다.
3) Cochrane-Orcutt Method


CO방법은 아무 ρ값으로 시작하여 LS estimator를 구한 뒤, 이를 통해 ρ값을 추정한다. 이를 다시 사용하여 LS estimator를 구하고.. 반복하여 ρ를 가능한 적은 변동치를 갖도록 구하는 방법이다.
6. Prediction with AR(1)

E(ei)일 때는 Yt를 Yt+1 추정에 활용할 필요가 없으나, 자기상관이 존재하는 모형에서는 Yt 모형을 통해 et를 구하고, 이를 Yt 추정치에 사용해야만 OLS를 돌릴 수 있다.

7. Other forms of Autocorrelation


이동평균법을 사용하면 자기상관의 문제가 발생한다.
이동평균은 error term에 t와 t-1시점의 white noise가 함께 물려있어서 자기상관이 발생한다.
그러나 MA(1)의 경우에 s가 1이 아닌 수라면 Et와 Et-s간의 공분산은 0이 되어 자기상관성이 없다.
따라서 이 경우엔 이전과 같이 s가 무한히 늘어도 그 영향력이 사라지지 않는 AR(1)의 경우와 달리, 충격이 발생해도 그 충격이 MA(n)의 경우 n을 넘기지 않는다. 따라서 MA(1)의 경우엔 t+2시점부터는 상관계수가 0이 되어 영향력이 전혀 없다. memory size가 1인 것이다.



ARMA의 방식도 존재한다. AR과 MA의 형태가 Et에 내장된 모습이다. 나중에 관련 내용을 업로드하겠다.
8. Examples

GDP가 소비에 미치는 영향을 확인하기 위해 시계열 데이터를 OLS 돌려본 결과다.
p-value가 매우 낮고 결정계수값이 높아 매우 유의미한 결과로 인식된다.
그러나 DW test의 값이 0.3001인데 이를 DL, DU값과 비교하여 자기상관성의 유무를 판단할 필요가 있다.
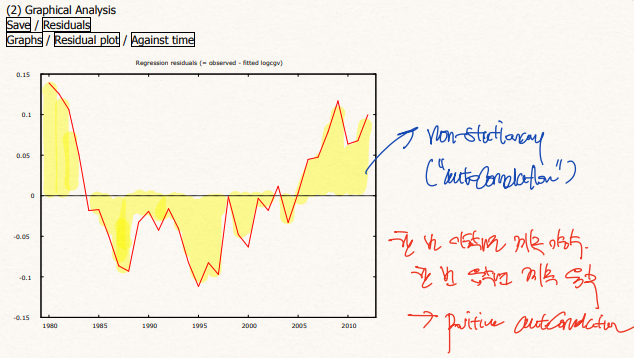

우선 육안으로 확인했을 때 잔차가 non-stationary한 형태를 가진다. 만약 stationary하다면 매우 랜덤하게 0을 기준으로 왔다갔다 해야하는데, 한번 양수면 계속 양수, 한번 음수면 계속 음수가 지속되는 postitive autocorrelation을 의심할 수 있다.
마찬가지로 et와 et-1간의 rho값도 0.807로 그 자기상관성이 매우 높음을 확인할 수 있다.

이를 객관적으로 검증하기 위해 DW-test를 사용한다.
D(n=33, k'=1)(k'는 상수를 제외한 설명변수의 수)가 dL=1.383, dU=1.508이다.
이 때 D값은 dL보다 훨씬 낮기 때문에 rho가 1과 유사한 수임을 확인할 수 있고, 따라서 자기상관성이 존재하지 않는다는 귀무가설을 기각한다.

LM은 결정계수와 표본크기 n=33을 곱하여 도출한다. TR^2이 20.3465이고, 카이제곱분포의 critical value가 이보다 작을 확률이 0에 수렴하기 때문에 가설은 기각된다.

마지막으로 rho와 estimator를 구하기 위한 CO Method다. rho값과 DW-test의 D값이 많이 변화한 것으로 보아 자기상관성이 크게 줄어든 값들이라 유추할 수 있다.
'계량경제학 > 계량경제학' 카테고리의 다른 글
| [계량경제학] 11. Heteroscedasticity (0) | 2021.12.09 |
|---|---|
| [계량경제학] 9. multiocollinearity (0) | 2021.12.08 |
| [계량경제학] 10. Dummy Variable Model (0) | 2021.12.08 |
| [계량경제학] 8. model specifications (0) | 2021.12.08 |
| [계량경제학] 7. multiple regression model (0) | 2021.12.08 |



