
Relation(관계)에 대해 알아보자.
A가 공집합이 아니라면, '관계'는 순서가 정해진 A 내부 원소의 pair를 뜻한다.
예를 들어 A가 모든 정수들의 집합이라면 (1,2), (1,3), (0,3), (-1,4)를 원소로 갖는 R은 A와 A 사이의 relation이다.
원소간의 순서가 존재하기 때문에 이는 relation이라 봐야한다. 가령 (1,2)은 R에 속하는 원소지만, (2,1)은 아니다.

(1,2)가 R의 원소라면, 1은 2에 related되어있다고 표현한다. 그러나 2가 1에 related된 것은 아니다. (2,1)이 R의 원소가 아니기 때문이다. 아래 2번 예시도 같은 얘기를 담고 있다.
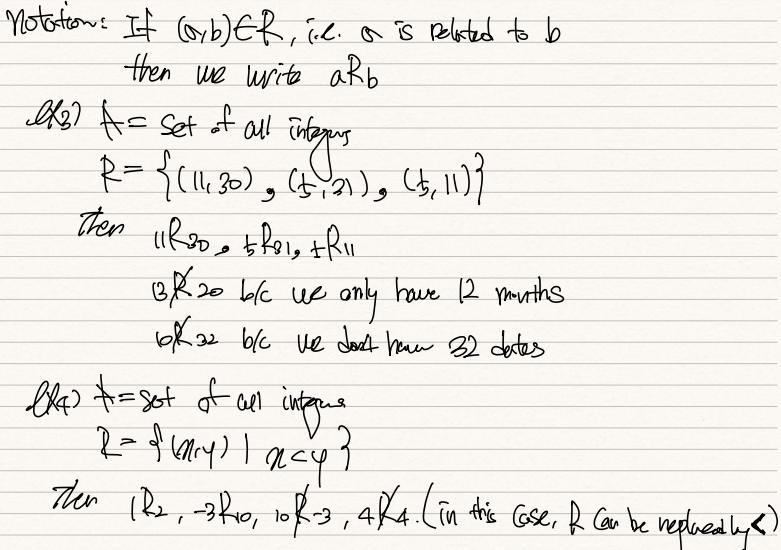
(a,b)가 R의 원소라면, 즉 a가 b에 related되어있다면 aRb로 표현한다.
4번 예시를 살펴보면, 이 때 R의 paired element인 x,y는 A에 속하는 모든 정수이며, 이들 중 x < y인 것들이 (x,y)로 R에 속한다는 뜻이다. 따라서 1R2, -3R10은 R에 속하지만, 10R-3은 안된다. 0.1R10은 x<y의 조건에는 부합하지만 0.1이 정수가 아니기에 포함되지 않는다.

inverse relation, 즉 역관계는 R ^ -1로 표현된다. 이는 말그대로 R에 속한 paired element의 순서가 바뀐 것들을 포함하는 집합이다.
4번 예시를 살피면 x<y의 조건을 만족하는 R의 역관계는 x>=y가 아님을 보이고 있다. R={(1,2),(2,3)...}에 (2,2), (1,1)이 애시당초 포함되지 않기 때문에 R 원소의 순서를 뒤집은 R 역관계에는 당연히 (2,2), (1,1) 등의 원소는 존재하지 않는다.

R 역관계의 역관계는 원래 R이다.

R이 집합 A에 대해 정의된 relation이라 가정할 때,
1) A의 모든 원소 x에 대해 xRx라면 R은 reflexible하다
2) 특정 (x,y)에 대해 만약 xRy이고, yRx라면, R은 symmetric하다
3) 특정 (x,y)에 대해 만약 xRy, yRz이고 xRz라면, R은 transitive하다.
이 특성들은 서로에 대해 독립적이기 때문에 특정 특성의 충족이 다른 특성의 충족을 뜻하지 않는다.
예를 들어 살펴보자.
예시1의 R은 reflexible한가? A집합 내 모든 원소 x에 대해 xRx여야 하기 때문에 3R3이 없는 R은 reflexible하지 않다.

1번예시: Rx/Sx/To
2번예시: Rx/So/Tx
3번예시: Rx/Sx/To
4번예시: Ro/Sx/To
간단한 예시로 확인해보면 쉽다.

5번예시: Ro, So, Tx
x=y인 경우도 R에 포함되니 xRx다.
|x-y|=|y-x|이기에 symmetric이다.
0R1, 1R2인데 0R2은 아니기에 transitive는 아니다.
6번예시: Rx,So,To
(3,3)이 없으니 Reflexive는 아니다.
(1,1) => (1,1)도 symmetric이다.
(1,1) => (1,1) => (1,1)도 transitive다.

만약 R이 symmetric하다면 inverse of R = R이다.
증명) R이 symmetric하다고 가정하자. 그렇다면 우리는 inverse of R과 R이 상호 포함관계에 놓여있음을 보이면된다.
for all xRy, R이 symmetric하기 때문에 yRx다. yRx는 inverse of R의 definition에 의해 xRy가 inverse of R에 속한다.
따라서 R은 inverse of R에 속한다.
inv of R에 속하는 (x,y)에 대하여 (y,x)는 inv의 정의에 의해 R에 속한다. (x,y)는 R이 symmetric이기에 R에 속한다. 따라서 inv of R은 R에 속한다.
아래 예시처럼 inv of R이 symmetric이면 inv of R은 R과 같다.


만약 R이 reflexive, symmetric, transitive하다면 R을 equivalence relation이라한다.
n을 양의 정수라고 가정해보자. 우리는 mod n일때 x가 y에 대해 congruent(합동)이라 한다. x≡y (mod n)
x-y // n = 0인 경우다.

A가 정수집합일 때, 양의 정수 n이 있다고 가정하자. R={(x,y)|x≡y(mod n)}은 equivalence relation이다.
for all x in A, x-x=0=0*n 이라 reflexive
for all x,y in A, if x-y = t*n then y-x = -t*n이라 symmetric이다
if x≡y, y≡z (mod n)이라면, x-y = t*n , y-z = s*n이다. 연립방정식으로 풀어내면 x-z = (t+s)*n이기에 x≡z다.
따라서 x≡y(mod n)인 (x,y)를 담은 Relation은 equivalence relation이다.

R이 equiv. relation on A다.
for all a in A, equiv class of a를 [a]로 표기한다. [a]는 for all x in A, xRa인 집합이다.
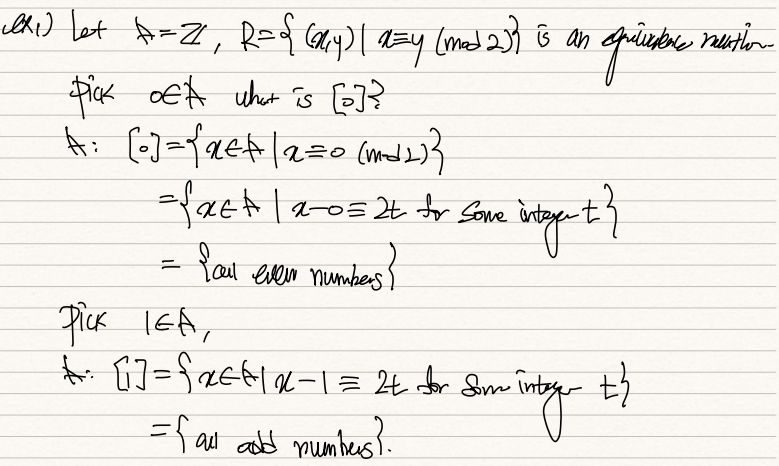
[0]은 for all x in A, xR0인 집합이다.
그런데 R의 정의가 {(x,y)|x≡y(mod2)}이기 때문에 x는 모든 even number다.
[1]은 (x-1) = 2*s 여야 하기 때문에 x는 all odd number다.

위와 같이, mod 7에 대해선,
[0]은 all int divisible by 7,
[1]은 all int divisided by 7 has reminder 1... 의 구조를 갖는다.
mod n의 R에 대해선 n개의 equiv class가 존재한다.

한번 훑어보자.

자 여기서 잘 알아둬야할것이, [x]는 xRy인 y의 집합이다. 따라서 uRv의 관계에 있던 모든 v(in R - {0})이 equiv. class의 원소가 된다.


prop1. R이 equiv. relation이라면, A의 모든 원소 a에 대하여, a in [a]다.

prop2. R이 A에 대해 equiv. relation일 때, a,b in A에 대해 aRb iff [a] = [b]이다.
R이 equiv relation이기 때문에, aRb라면 bRa다. 따라서 [a]에는 {a,b}, [b]에는 {a,b}가 있어야만 한다.

prop3. [a],[b]의 교집합이 공집합이 아닐때, [a]=[b]다.
공집합이 아니란 가정이기에, x in [a] and [b]는 equiv class의 정의에 의해 xRa, xRb다.
symmetric에 의해 xRa, aRx, xRb, bRx이다.
transitive에 의해 aRx, xRb, aRb다.
aRb라면 [a] = [b]다.

만약 [a] != [b] 라면, [a],[b]의 교집합은 없다.
'수학 > 이산수학(Graph Theory)' 카테고리의 다른 글
| [이산수학] (6) Subgraphs (0) | 2022.04.20 |
|---|---|
| [이산수학] (5) Handshaking Lemma (0) | 2022.04.20 |
| [이산수학] (4) Fundamentals of Graph Thoery (0) | 2022.04.20 |
| [이산수학] (3) Partition (0) | 2022.04.20 |
| [이산수학] (1) Recurrence Relation (0) | 2022.04.17 |



