
edge가 교차되지 않고 그릴 수 있다면 G는 Plannar이다.
Euler's Formula)
G가 connected graph일 때, 교차되지 않은 형태의 그림을 고르자.
이 때 우린 |V(G)| - |E(G)| + |F(G)| = 2 의 식을 얻는다.


pf) 만약 G가 connected graph이고 f=1인 crossing free 그림이 있다고 가정해보자.
이 때 G는 cycle이 없기 때문에(f=1이라서) G는 Tree다.
Tree의 Prop에 의해 |E(G)| = |V(G)| - 1 이고, n-m+f = 1 + f = 2로 Euler's Formula가 f=1일 때 참이다.

수학적 귀납법으로 f=k일 때 Euler's Formula가 성립한다고 가정하고,
f=k+1인 G를 다뤄보자. f=k+1 >= 2이기 때문에 G는 cycle을 갖는다.
이 Cycle의 edge e를 골라서, G-e를 그린다면,
|F(G-e)| = |F(G)| -1
|V(G-e)| = |V(G)|
|E(G-e)| = |E(G)| -1 이다.
이 경우 G-e는 k개의 face를 갖기 때문에,
|V(G-e)| - |E(G-e)| + |F(G-e)| = 2이고,
이는 곧 |V(G)| - (|E(G)|-1) + (|F(G)|-1) = 2이다. 식을 풀면 |V(G)| - |E(G)| + |F(G)| = 2 이니까
수학적 귀납법이 성립한다.

crossing free 그림을 골랐을 때, F(G)는 모든 face의 set을 나타낸다.
이 때 특정 face의 degree는 그 face를 둘러싼 edge의 갯수나, face가 둘러싸고 있는 edge의 갯수를 뜻한다.
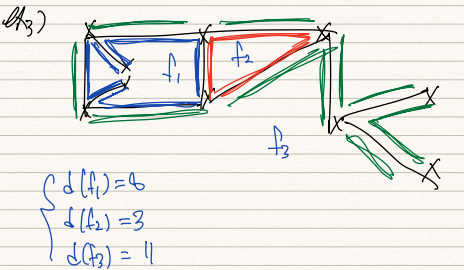
double counting도 된다.

prop) Handshaking Lemma for faces
G가 plannar rgaph일 때, G의 crossing-free 그림을 골라보자.
이 떄 sigma sum of d(f) = 2|E(G)| 이다.
왜냐면 안 밖으로 double counting 되니까...
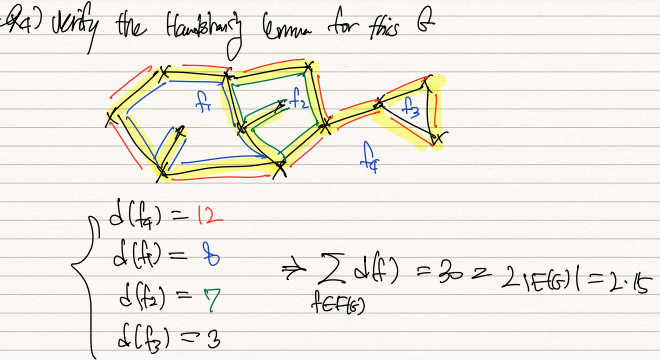

cor1) G가 최소 2개 이상의 edge를 가진 Plannar Graph일 떄,
|E(G)| <= 3 * |V(G)| - 6 이다.
pf) case1 : G가 connected인 경우 Euler's formula에 의해 |V(G)| - |E(G)| + |F(G)| = 2를 얻고,
Handshaking Lemma로 2|E(G)| = sigma sum of d(f)를 얻는다.
마지막으로 for f in F(G), d(f)>=3이기 때문에(edge가 2개이상이니까!)
2|E(G)| >= sigma sum of 3 = 3|F(G)|다.
이를 Euler's formula에 대입하면, 2 - |V(G)| + |E(G)| = |F(G)| <= 2/3 |E(G)| 이다.
이는 곧 |E(G)| <= 3|V(G)| - 6이다.
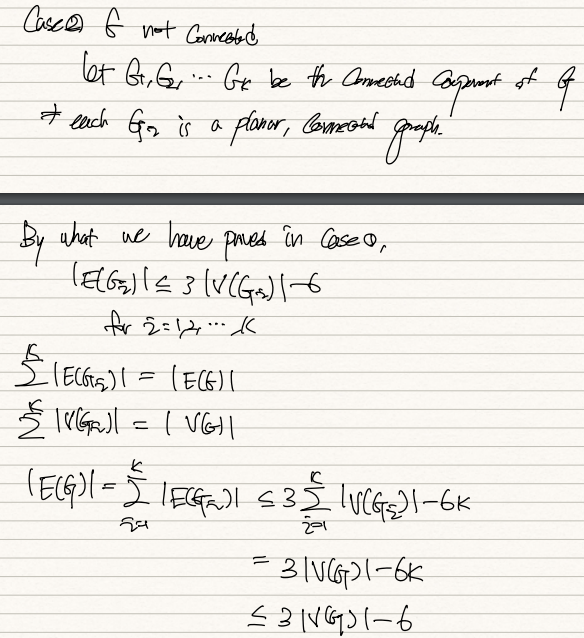
case2: G가 connected가 아니라면 G1, G2, ... Gk가 connected comp of G라고 가정해보자.
각자의 Gi는 이경우 plannar이고, connected graph일테다.
그럼 각자의 경우에 대해 |E(Gi)| <= 3*|V(Gi)| - 6을 진행하고 모두 sum up하면 같은 결과가 나온다.


def) girth는 g(G)로 표기되며, G의 cycle 중 가장 작은 length를 뜻한다.

cor) |E(G)| <= g/(g-2) * |V(G)| - 2g/(g-2) 다.
pf) case1: G는 connected이고, Euler's Formula와 Handshaking Lemma로 들고오고
g(G0 = g, d(f) >= g를 가져올 때, 2|E(G)| >= g*|F(G)| 이고, euler's formula와 결합할 경우
2 - |V(G)| + |E(G)| = |F(G)| <= 2/g |E(G)| 이다. 잘 풀어쓰면 나온다.
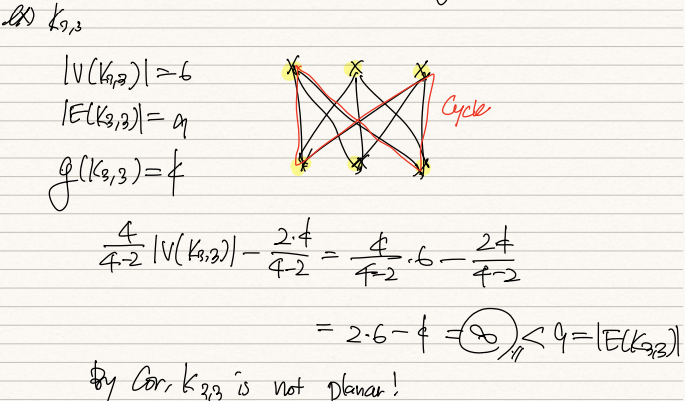
g=4, n=6, m=8 : ㅏ3,3은 plannar가 아니다.

요약정리)
1) 그 어떠한 subgraph of G가 plannar이면 G는 plannar다.
2) 단 하나라도 plannar가 아닌 subgraph가 있다면 G는 plannar가 아니다.
3) G가 K5의 subdivision을 담고 있다면 G는 plannar가 아니다. Kn (n>=5)는 plannar가 아니다.
4) K3,3을 subgraph로 갖는 G는 plannar가 아니다. m,n >=3인 Km,n은 전부 plannar가 아니다.

def) subdivision of G는 edge들을 path로 대체한 것이다.
Kuratowski Thm) plannar가 아니다 iff G가 subdivision of K5 혹은 K2,3을 subgraph로 갖고 있다면,
'수학 > 이산수학(Graph Theory)' 카테고리의 다른 글
| [이산수학] (13) Coloring & Poset (0) | 2022.06.14 |
|---|---|
| [이산수학] (11) Coloring (0) | 2022.06.14 |
| [이산수학] (10) Tree & Spanning Tree (0) | 2022.06.14 |
| [이산수학] (9) Dirac's Thm (0) | 2022.06.14 |
| [이산수학] (8) Eulrian Graph (0) | 2022.06.13 |



