
G의 Crossing #은 G에 대한 모든 drawing 중 최소의 Crossing 이다. 이는 Chromatic Number라 부르며, Cr(G)로 표기한다.
G가 Plannar이면 Cr(G)=0, 아니면 >=1

그림으로 Cr(G)<=1 인것을 증명하면 제일 좋다. Cr(G)=1로 확정되기 떄문

Cr(Kn) = 1/4 lower(n/2)*lower(n-1/2)*lower(n-2/2)*lower(n-4/2) (n <=12)
Cr(Km,n) = lower(m/2)*lower(m-1/2)*lower(n-1/2)*lower(n/2) (m <=6)

Cr(K2,4,n) >= lower(n/2)*lower(n-1/2) + 2n
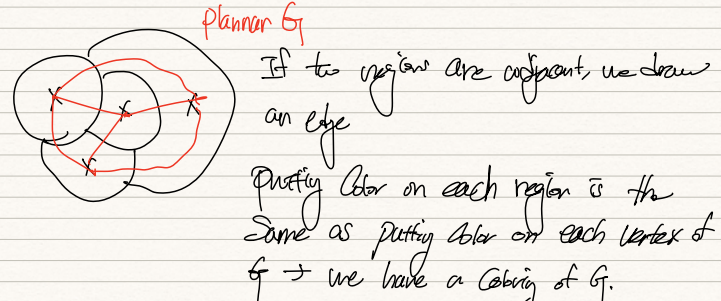
Coloring 문제는 Graph로 변환하면 쉽다.
Region에 색칠하는 것은 Vertices에 색칠하는 것과 같기 떄문.

<4 color Problem>
어떠한 Plannar Graph도 4-coloring이면 된다.
*이 때 Plannar Graph는 fully connected된 graph가 아님!
Thm) del(G) <=5인 어떠한 Plannar Graph도 6-coloring이면 충분하다.


partially orderd to sets
def) poset은 P=(X,R)의 pair이다. X는 set이고 R은 X에 대한 relation인데, 이는 다음을 충족한다.
R은 reflexive, anti-symmetric, transitive
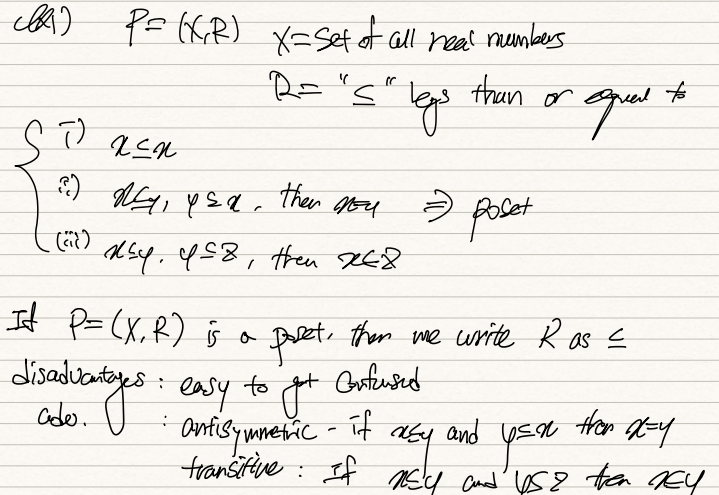

Hasse Diagram) poset P의 structure를 이해하기 위해 그리는 다이어그램이다.
Relation : Divides

<= = "포함관계" 인 경우...
height = 4, width = 3





'수학 > 이산수학(Graph Theory)' 카테고리의 다른 글
| [이산수학] (12) Plannar (0) | 2022.06.14 |
|---|---|
| [이산수학] (11) Coloring (0) | 2022.06.14 |
| [이산수학] (10) Tree & Spanning Tree (0) | 2022.06.14 |
| [이산수학] (9) Dirac's Thm (0) | 2022.06.14 |
| [이산수학] (8) Eulrian Graph (0) | 2022.06.13 |



