
primal problem은 y = WX + e 인 함수다. 이 함수의 error term을 최소화해주고 싶다.
따라서 f(x) = (y-WX)^2를 objective function으로 설정한다.

우리는 Newton's Method를 통해 objective function을 optimize하려고 하는데, 이 optimize란 이 경우에 한해 LS를 최소화해주는 것을 뜻한다. f(x)가 최소화되기 위해선 f'(x) = 0인 x*를 찾으면 된다. Newton's Method는 이런 점을 공략한 알고리즘이다.
이게 표기가 다소 복잡해졌는데 원함수(least square function)를 F(x)라고 설정하고, F(x)의 1계도함수를 f(x)라 표기하겠다.
우선 주어진 시점 x0에서 f(x)의 도함수값인 f'(x0)를 구하고, y=f'(x0)(x-x1)를 통해 x1값을 구한다. x1의 함수값은 그러면 x0에 비해 비교적 0에 가까워진다. 이러한 과정을 recursive하게 계속 반복해주면 언젠가는 f(x*) = 0이 되는 optimal solution x*를 구할 수 있게 된다. 이 식을 일반화하면 위와 같다.

그럼 Newton's Method는 ML개론에서 살펴본 gradient method과 무엇이 다른가?
사실 idea는 거진 유사하다. 그러나 gradient method는 learning rate를 직접 지정할 수 있는 반면, newton's method는 inverse of f'(x)로 고정되어있단 점에서 다르다.
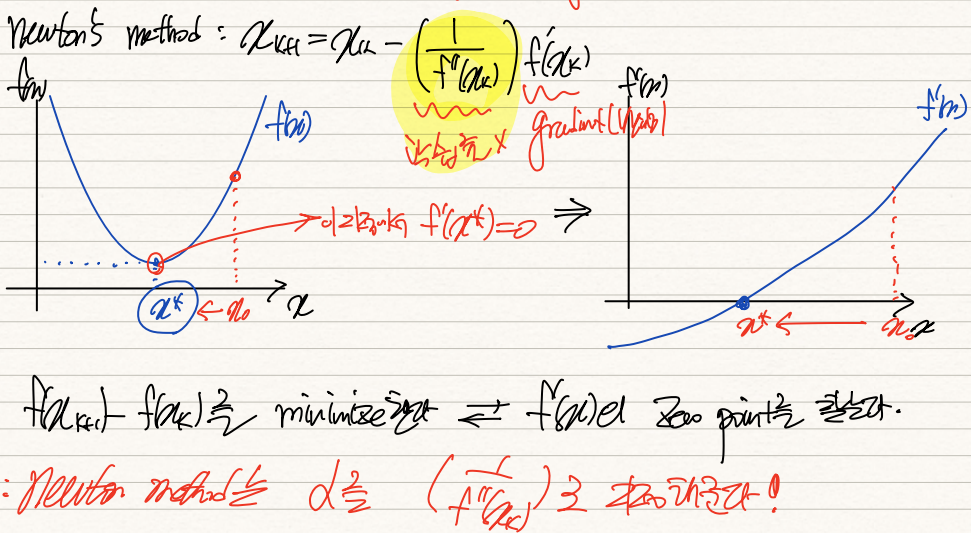
둘 사이 큰 차이점이 없는 것이 그 idea가 거진 똑같기 때문이다.
gradient method는 결국 천천히 내려가면서 f(x_k+1) - f(x_k)가 0에 수렴하는 x*를 찾는 과정이다.
Newton's method는 f'(x)=0이 되는 x*를 찾는 과정이다.
f(x_k+1)-f(x_k) / (x_k+1 - x_k) = f'(x) 라는 점에서 둘은 사실상 같다.

Newton's Method에서 learning rate는 f'(xk)로 지정되어있는데 이는 원함수 F(x)의 2계도함수, vector field의 경우 Hessian Matrix다.


그러므로 이전의 식을 위와 같이 유도할 수 있다.
식을 추가적으로 더 전개하다보면 x_k+1 = (pseudo inverse of W) * Y 임을 알 수 있는데 이는 일전에 살펴본 least square solution의 closed form과 동일하다. least square solution의 경우 W, Y만 알고 있다면 바로 optimal solution x*를 찾을 수 있다는 점에서 gradient method, newton's method에 비해 우월한 것처럼 여겨진다.
그러나 f(x) = WX와 같은 선형적 관계가 아니라 logistic function과 같은 비선형적 함수가 f(x)로 주어지면 closed form solution을 사용하지 못하게 된다. 이 때 우리는 Newton's method와 gradient method를 사용한다.
여기서 또 Newton's method는 gradient와 달리 learning rate를 지정해주니까 더 우월하다고 판단할 수 있는데 사실은 그렇지 않다. Newton's method는 기본적으로 Hessian mtx를 구해줘야하고 거기에 inverse까지 구해야하니 처리해야할 연산량이 어마무시하다. 그에 반해 gradient는 딱 gradient만 구하면 되니까 연산이 비교적 수월하다. 따라서 특정 방법이 우월하다거나 그렇진 않다. 적재적소에 알맞은 방법론이 쓰일 뿐이다.
'기계학습 > Optimization' 카테고리의 다른 글
| [최적화] (5) Symmetric Rank-one Update(SR1) (0) | 2022.02.05 |
|---|---|
| [최적화] (4) Broyden's Method (0) | 2022.02.05 |
| [최적화] (3) quasi Newton Method (0) | 2022.02.05 |
| [최적화] (0) scalar를 vector로 미분 (0) | 2022.02.04 |
| [최적화] (1) Convex Optimization Problem (0) | 2022.02.04 |



