최적화 이론을 다루기에 앞서 scalar를 vector로 미분하는 경우, vector를 vector로 미분하는 경우, scalar를 matrix로 미분하는 경우를 다뤄보겠다. 이들은 Newton's Method나 KKT 등 최적화이론을 다룸에 있어 좋은 무기로 기능한다.
시작에 앞서 유튜브 혁펜하임(https://www.youtube.com/channel/UCcbPAIfCa4q0x7x8yFXmBag)님의 강의를 참조하여 작성한 글임을 밝힌다. 사실 필기자료의 가독성이 많이 떨어지고 전달력에 한계가 있으니 강의 수강을 권한다.
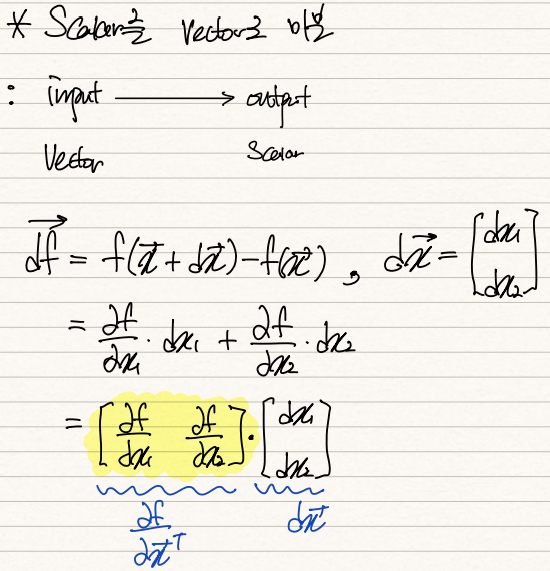
우선 scalar를 vector로 미분하는 경우다.
함수 f가 vector <x1,x2>를 input data로 받는데 f(X) = WX+b 값이 scalar값인 경우에 활용된다. 이 경우 input data <x1,x2>의 움직임에 따른 f(x)의 변화량 관찰을 할 수 있다.
df = grad(f_x) * dx 로 구성된다. 우리는 grad(f_x)를 알고 싶은 것이니 df 수식 전개를 통해 grad(f_x)에 접근한다.
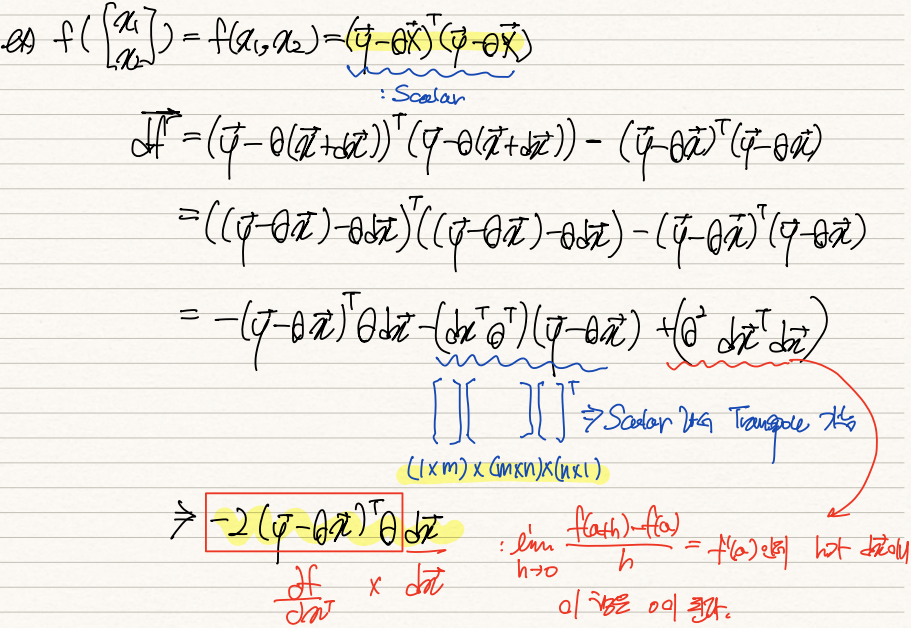
사실 vector를 input으로 받고 scalar를 반환하는 함수 중 대표적인 예시가 OLS function이다. 이 함수는 실제값 y에 예측값 WX(theta 표기가 힘들어 theta를 W로 적겠음)를 차감한 (error term)^2를 반환한다.
df = f(x+dx) - f(x)을 전개해주면 셋째 줄의 수식이 유도된다. 둘째 항은 scalar이기 때문에 transpose를 취해주어도 그 값에는 영향을 주지않으니 Transpose를 취해주고, 셋째항은 잘보면 dx^2의 형태기 때문에 dx를 0으로 보내주면서 항 전체가 0이 된다. 따라서 df는 -2(y-WX)W*dx의 형태로 정리된다. df = grad * dx 이기 때문에 dx를 뺀 부분(=-2(y-WX)W)이 우리가 원하는 grad f(x)이다.

두번째는 vector를 vector로 미분해주는 경우다.
이전 예시에서 살펴봤듯이 함수값(scalar)를 vector로 미분할 경우 행벡터 형태의 -2(y - WX)^T W가 도출된다.
이 vector를 또다시 vector로 미분하면 2계도함수를 원소로 품는 Hessian matrix가 도출된다.
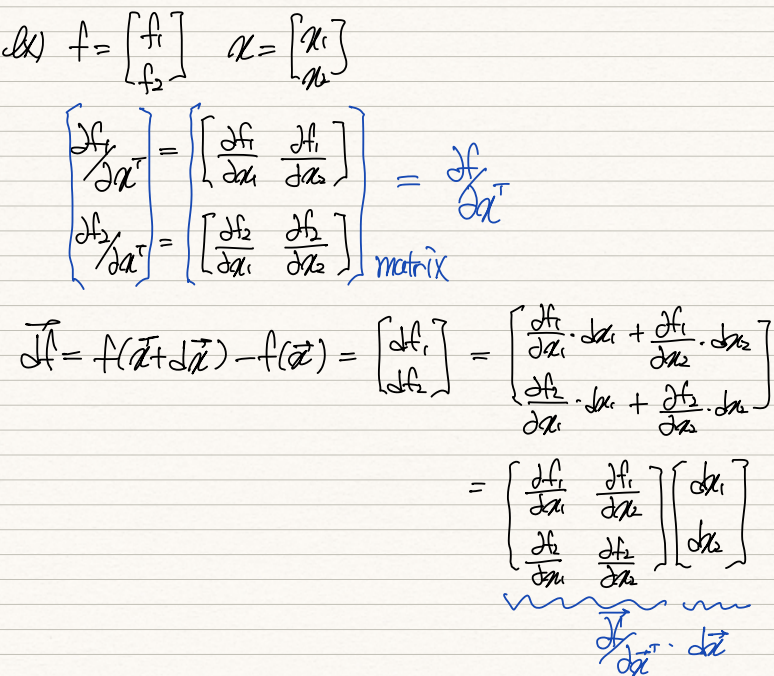
앞서 살펴본 scalar를 vector로 미분해준 경우의 결과값이 열벡터라는 점에서, 이를 <f1, f2>로 표현할 수 있다. <f1, f2>를 <x1, x2>로 미분해주는 것은 사실 각각 따로 미분해준 vector를 matrix의 형태로 쌓아올린것과 같다.
df = <df1, df2>인데 이는 af/aX * dx로 분할 가능하다. 이 af/aX를 우리는 Hessian Matrix라 부른다.


헷갈려서 정리해보자면 다음과 같다. 반환값이 scalar의 형태인 f에 대해 vector X로 미분할 경우 빨간색 박스처럼 나온다. 이 vector는 행벡터의 형태기 때문에 이를 열벡터의 형태로 변환해주기 위해 Transpose를 취해준다. 이 전치된 af/aX를 새로이 g(x)로 정의한다. 그리고나서 이를 다시 vector X로 미분하면 ag/aX가 도출된다.
이 ag/aX를 df = ag/aX * dx의 식을 통해 구한다. 식을 전개하면 (2W^2) dx 가 도출되는데 이 때 2W^2를 우린 Hessian Matrix라 부른다.

마지막으로 scalar를 matrix로 미분하는 경우다. input data 자체가 matrix인 경우도 있을 수 있다.
이 때 af/aX를 구하기 위해 기존처럼 df를 사용하면 뜻대로 잘 되지 않는데 이 때 trace를 사용한다. transpose of af/aX에dx matrix를 곱해 생성한 matrix 중 diagonal 원소만을 추출해 df를 구성하는 것이다. df = tr(grad * dx)이기 때문에 grad는 transpose of af/aX가 된다.
위 세가지 tool을 활용하여 ML과 최적화에서 등장하는 온갖 수식의 해답을 찾아낼 수 있다.
'기계학습 > Optimization' 카테고리의 다른 글
| [최적화] (5) Symmetric Rank-one Update(SR1) (0) | 2022.02.05 |
|---|---|
| [최적화] (4) Broyden's Method (0) | 2022.02.05 |
| [최적화] (3) quasi Newton Method (0) | 2022.02.05 |
| [최적화] (2) Newton's Method (0) | 2022.02.04 |
| [최적화] (1) Convex Optimization Problem (0) | 2022.02.04 |



