이전 게시글에서 살펴본 Infeasible Start Newton's Method을 실제로 활용할 때는 W_k+1 = Wk - t*(R(w)/R'(w))로 업데이트해준다. 차이점은 t가 붙었다는 것인데 이 t는 Backtracking Line Search를 융합해준 결과다. 그렇다면 Backtracking Line Search는 어떠한 tool인지 알아보자.
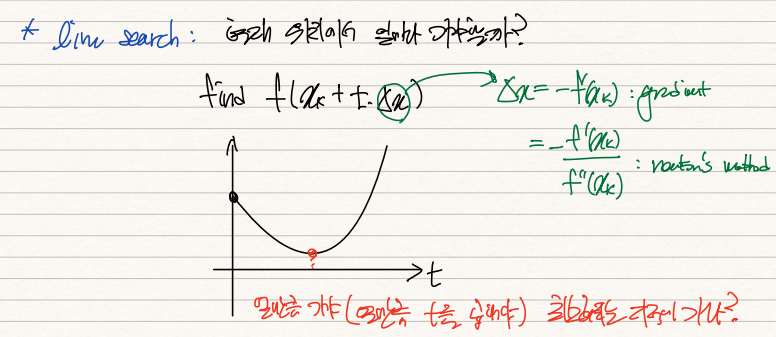
우선 Backtracking을 알기 이전에 Line-Search의 개념을 짚고 넘어갈 필요가 있다.
Line Search는 주어진 del x, 즉 newton's method에선 -f'(xk)/f''(xk), gradient method에선 -f'(xk)에다가 상수 t만큼 곱하여 알고리즘을 돌리는 방법이다. 가령 t=0이면 움직이지 않는 것이니 f(xk)에 머물러있고, t가 큰 숫자면 지나치게 많이 이동하게 되어 optimal sol을 얻지 못하게 된다. 따라서 del x가 x의 방향을 정해준다면 t는 그 보폭의 크기를 지정해준다.
이 지점에서 개인적으로 의문이 들었던 것이 gradient method는 학습률에 대한 정의가 없으니 t를 지정해주는 것이 자연스러워 보였는데 newton's method는 learning rate를 inverse of f''(xk)로 지정해줬음에도 불구하고 왜 t를 추가적으로 지정해주는가? 였다.
*관련내용: https://alba-tross.tistory.com/77?category=999369
이게 깔끔하게 optimize되는 2차함수로 예시를 들면 이해가 잘 가지 않지만 고차함수를 예시로 들면 이해가 잘된다. 가령 3차함수 x^3-3x를 원함수로 설정하고 x0=0.99로 설정하고 -f'(xk)/f''(xk) 작업을 해주면 local min인 x=1을 넘어서게 된다. 4차, 5차 등 고차함수로 갈수록 initial point의 설정에 따른 optimal solution 수렴 여부가 결정되기 때문에 t에 대한 설정이 필수적이라 할 수 있겠다.
Line search는 [0,1] 사이의 수백개의 t를 대입하여 f(x)값이 최소화되는 t를 찾아낸다. 그러나 이 방법은 연산이 지나치게 많아지기 때문에 다소 비효율적이다. 따라서 도입된 것이 Backtracking Line Search다.

1차 taylor series를 통해 f(xk+t*Δx)를 근사한다면 이는 f(x) + af/at * t로 표현된다.
이 때 af/at는 chain rule에 의해 df(xk+tΔx)/d(xk+tΔx) * d(xk+tΔx)/dt로 전개 가능하고, t=0에서 앞항은 f'(xk) 뒷항은 Δx가 되어 t=0에서의 t축에 대한 함수 f(x)의 기울기로 표현된다.
자 그러면 f(xk)는 t=0일 때의 값이니 t축에서는 y절편으로서 기능하고, f'(xk)*Δx는 t=0에서 f(xk+tΔk)의 기울기값이니 이 둘의 합은 빨간색 선과 같이 표현된다.

이렇게 구한 t=0에서의 기울기를 (0, 1/2) 사이의 값 alpha로 곱해주면 위 그림에서의 녹색선과 같이 그려진다. 기울기가 더욱 완만해졌으므로 보통 f(x)와 접점을 형성하게 되는데 t에 대한 정확한 정보가 없으니 알고리즘을 통해 t=1부터 원함수값<녹색선이 되는 t지점을 찾는다. t값을 update하기 위한 beta를 설정하고 파란선<녹색선이 될 때까지 beta값을 업데이트해나가면 드디어 t*를 찾게된다.
그러면 이 t가 가장 optimal한 t값은 아니더라도 적당한 보폭을 구할 수 있게 되고,
이 t를 기반으로 X_k+1 = Xk + t*Δx를 업데이트하면 optimal solution값이 발산하지 않는 적절한 값을 구할 수 있다. 일반적으로 이러한 backtracking line search를 통해 적절한 보폭 t*를 먼저 구하고, newton's method나 gradient method를 푼다.
'기계학습 > Optimization' 카테고리의 다른 글
| [최적화] (11) solving dual problem with KKT (0) | 2022.02.21 |
|---|---|
| [최적화] (10) KKT condition (0) | 2022.02.21 |
| [최적화] (8) Infeasible Start Newton's Method (0) | 2022.02.21 |
| [최적화] (7) Lagrangian Multiplier Method (0) | 2022.02.21 |
| [최적화] (5) Symmetric Rank-one Update(SR1) (0) | 2022.02.05 |



