
Lagrangian을 복습해보면 위 두 조건이 optimal solution의 필요조건이었기에 이를 만족하는 lambda를 찾으면 x*를 구할 수 있었다.

그럼 위 수식과 같이 inequality constraint가 존재하는 문제의 필요조건은 무엇인가? 바로 KKT다.
KKT는 총 5가지로 구성된다. stationarity, complementary slackness, dual feasibility, primal feasibility가 바로 그것이다.
이 5가지 조건을 모두 만족하는 lambda, mu가 존재하는데 이를 구하면 x*를 얻을 수 있다.
그런데 3,4,5번에 해당하는 feasibility condition은 사실상 주어지는 것과 마찬가지다. g(x*)<=0, h(x*)=0이 constraint이기 때문에 이는 primal feasiblity이고, mu 또한 기하적으로 고려해보면 stationary를 충족시키기 위해서는 mu>=0이어야만 한다.
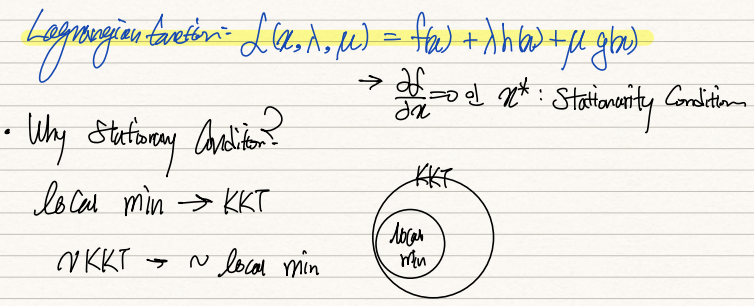
그럼 stationarity와 complementary slackness만 판단하면 되는 문제로 귀결된다. 하나씩 살펴보자.
우선 Lagrangian fn은 f(x)+λh(x)+μg(x)로 재정의된다. inequality constraint인 g(x)에 μ가 곱해진 형태로 더해진 것이다. Lagrangian fn을 x로 편미분했을 때 aL/ax=0을 만드는 x*를 찾을 수 있다면 stationarity condition이 만족된다.
'모든 극소점은 KKT를 만족한다'는 명제의 대우명제는 'KKT가 아니라면 극소가 아니다'이다. 그럼 KKT를 만족하지 않는 경우가 왜 극소가 아닌지를 기하학적으로 살펴보면서 이 명제를 이해해보도록 하자.

Lagrangian method를 공부할 때 살펴본 그 방법이 동일하게 적용된다.
feasilibty가 충족된 x*라면 이는 g(x*)가 최대 0이라는 뜻이다. 이 때 del g와 방향벡터 u가 둔각을 이룬다면(g의 방향도함수가 음수라면) g(x*)는 감소하니까 여전히 feasibility를 만족하게 된다. f는 우리가 minimize하려는 목적함수이니 del f와 u의 내적값이 음수라면 u방향으로 나아갔을 때 여전히 f가 줄어들 여지가 있다는 뜻이 된다.
따라서 특정 방향벡터 u에 대해 del g와 u가 둔각이고, del f와 u가 둔각이라면, 이는 g(x*)<=0의 feasibility가 지속적으로 충족되는 와중에 f(x)의 값이 더욱 minimize되는 것이니 u방향으로 가지 않을 이유가 없는 것이다.

그렇게 minimize되는 u방향으로 점진적으로 나아가다보면 del f와 del g는 필연적으로 평행선상에 놓이는데 이는 해당 지점에서 f,g가 공통접선을 가지기 때문이다.

그럼 inequality constraint인 g(x)를 충족했으니 equality constraint h(x)도 고려해봐야한다.
그런데 잘 생각해보면 del f와 del g를 고려하는 것이나 del L과 del g를 고려하는 것이 동일한 문제다.
del L=0을 만드는 x*은 h(x)=0 아래 f를 최소화하는 optimal solution이다. 그럼 Lagrangian fn을 최적화하는(aL/ax=0) x*가 f(x) 또한 최적화하니 del f 대신 del L을 이전과정에 대입해도 하등에 지장이 없다.
따라서 del L과 del g가 이전처럼 평행선상에 놓이게 되니 del f + λ*del h +μ*del g=0이 성립된다.

두번째 condition은 complementary slackness다. 이는 μ*g=0인 mu가 존재해야한다는 조건이다.
이는 g=0, g<0인 두가지 상황으로 양분하여 생각해볼 수 있다. g=0인 경계에 feasible solution이 존재한다면 mu는 0을 포함한 모든 양수값이 될 수 있다. g<0인 상황에선 mu=0가 필수적으로 성립해야한다.
mu=0이면 Stationarity condition에서 del f + lambda*del h = 0만 풀어주면 된다. 잘 고민해보면 g경계 위에서 optimal solution이 존재한다는 것은 f, h, g 모두가 동일한 공통접선을 가지기 때문에 이들 gradient가 평행선상에 놓인다는 뜻이다. 그러나 g<0이라면 del g는 사실 고려대상이 아니게 되므로 mu=0이 되는 것이다.

그러나 KKT 조건을 모두 충족한다더라도 optimal solution이 아닐 수 있다. given constraints들이 위 세가지 regularity condition 중 한가지를 만족하고, KKT를 충족하는 x*를 찾아야만 inequality constraint가 주어진 optimization problem을 해결할 수 있다.
LCQ는 h, g가 모두 affine fn, 즉 ax+b의 선형식이어야 한다는 조건이다.
LICQ는 feasibility를 충족하는 x*에서 g=0인 active ineqauility constraint와 equaility constraint가 서로 선형독립이어야 한다는 조건이다.
SC는 convex problem에 대해 h(x)=0, g(x)<=0 (if g is affine fn), g(x)<0 (if g is not affine fn)을 충족하는 x가 존재해야만 한다는 조건이다. 참고로 이 조건이 충족되었다는 것은 Strong duality를 충족했단 뜻이 된다.
'기계학습 > Optimization' 카테고리의 다른 글
| [최적화] (11) solving dual problem with KKT (0) | 2022.02.21 |
|---|---|
| [최적화] (9) Backtracking Line Search (0) | 2022.02.21 |
| [최적화] (8) Infeasible Start Newton's Method (0) | 2022.02.21 |
| [최적화] (7) Lagrangian Multiplier Method (0) | 2022.02.21 |
| [최적화] (5) Symmetric Rank-one Update(SR1) (0) | 2022.02.05 |



